Прежде чем начать изучать алгоритмы, нужно понимать, как оценивать их эффективность по времени и по памяти. Для этого используются так называемые асимптотические оценки. Они позволяют оценить время работы алгоритма в зависимости от размера входных данных.

Примеры

Во входном потоке даны $n$ целых чисел. Найдите их сумму.

1
2
3
4
5
6
7
8
int n;
cin >> n;
int sum = 0;
for (int i = 0; i < n; ++i) {
    int x;
    cin >> x;
    sum += x;
}

Такой алгоритм делает $n$ операций сложения и еще $n$ считываний. То есть мы можем грубо сказать, что алгоритм делает $2n$ операций. Опуская константу, мы будем говорить, что алгоритм работает за $O(n)$.

В то же время алгоритм требует всего две ячейки памяти, иначе говоря константу памяти. В таких случаях мы будем говорить, что алгоритм требует $O(1)$ памяти.

Во входном потоке даны $n$ целых чисел. Выведите их в отсортированном порядке.

Мы напишем простейшую сортировку, которая сначала находит минимальный элемент, затем второй по возрастанию и так далее.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int n;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; ++i) {
    cin >> a[i];
}

for (int i = 0; i < n; ++i) {
    int min_index = i;
    for (int j = i + 1; j < n; ++j) {
        if (a[j] < a[min_index]) {
            min_index = j;
        }
    }
    swap(a[i], a[min_index]); // поменять местами a[i] и a[min_index]
}

Оценим время работы алгоритма. Первый цикл на считывание совершает $n$ оперций. Теперь главная компонента алгоритма - сортировка: на первой итерации внешнего цикла алгоритм делает $n$ операций, на второй - $n - 1$, на третьей - $n - 2$ и так далее. Итого получается $n + (n - 1) + (n - 2) + \ldots + 1 = \frac{n(n + 1)}{2}$ операций плюс $n$ считываний из входного потока. Опуская константу и не-старшие слагаемые, мы будем говорить, что алгоритм работает за $O(n^2)$.

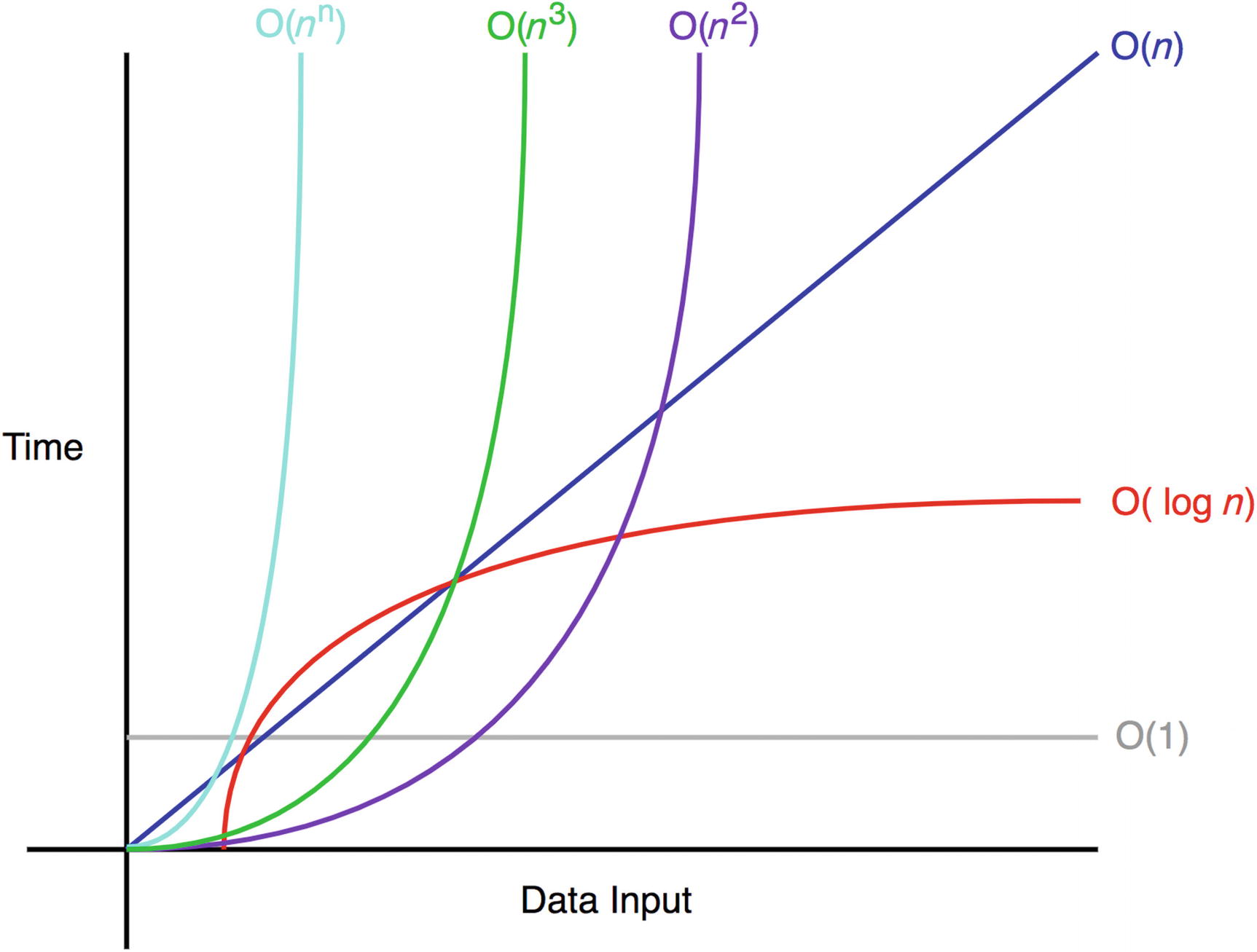
$O-$, $\Omega-$ и $\Theta-$нотация

Интуиция

На примерах выше вы уже поняли, что при оценке алгоритма по времени мы не учитываем константы, множители а так же учитываем только “самую большую степень” в алгоритме. Это неформально можно назвать “$O$ большое”. Кроме того, нас интересует случай “достаточно больших $n$”, поэтому мы не учитываем случаи маленьких $n$. В олимипадном программировании обычно используется именно такое “интуитивное” определение.

Но помимо $O$-оценки полезно знать об $\Omega-$ и $\Theta-$оценках. Все наши алгоритмы-примеры мы могли в точности оценить как $const \cdot n$ или $const \cdot n^2$, однако в общем случае нас может интересовать верхняя ($O$) и нижнаяя ($\Omega$) оценка времени работы алгоритма, если мы не можем в точности доказать время работы ($\Theta$-оценка).

Действительно, в теоретической информатике эти оценки часто пригаждаются в доказательстве теоретических свойств алгоритма, например мы можем предоставить доказательство того, что некоторую задачу нельзя решить быстрее чем за $\Omega(n \log n)$, но лучшее известное решение работает за $O(n^2)$. Это будет означать, что либо у нас слабая тоеретическая оценка, либо не оптимальный алгоритм.

Формально

Функция принадлежит множеству $O(g(n))$, если существуют положительные константы $c$ и $n_0$, такие что $0 \le f(n) \le c \cdot g(n)$ для всех $n \ge n_0$. Это означает, что $f(n)$ растет не быстрее, чем $g(n)$. Например, $n^2$ работает за $O(n^2)$, $n^2$ работает за $O(n^3)$, $n^2$ работает за $O(2^n)$. Все эти утверждения верны.

Функция принадлежит множеству $\Omega(g(n))$, если существуют положительные константы $c$ и $n_0$, такие что $0 \le c \cdot g(n) \le f(n)$ для всех $n \ge n_0$. Это означает, что $f(n)$ растет не медленнее, чем $g(n)$. Например, $n^2$ работает за $\Omega(n^2)$, $n^2$ работает за $\Omega(n)$, $n^2$ работает за $\Omega(\log n)$. Все эти утверждения верны.

Функция принадлежит множеству $\Theta(g(n))$, если она работает за $O(g(n))$ и за $\Omega(g(n))$. Это означает, что $f(n)$ растет так же, как и $g(n)$. Например, $100 n^2$ работает за $\Theta(n^2)$.

PS: Обычно вместо “принадлежит множеству” говорят “работает за”.

Упражнения

Упражнение 1:

Покажите, что $T(n) = n^2 + 2n + 1$ принадлежит $\Theta(n^2)$.

Упражнение 2:

Покажите, что \(f(n) = \begin{cases} 2^n, & \text{если } n < 100 \\ \log n, & \text{иначе} \end{cases}\) принадлежит $\Theta(\log(n))$.

Эти два упражнения должны дать вам понимание интуиции: мы не учитываем константы и множители и “случаи маленьих $n$”.

Упражнение 3:

Рассмотрим алгоритм, в котором есть следующий фрагмент кода:

1
2
3
4
5
for (int i = 1; i < n; ++i) {
    for (int j = i; j < n; j += i) {
        // что-то
    }
}

Покажите, что данный алгоритм работает $\Theta(n \log n)$.

Лучший, худший и средний случай

Кроме определения $O$, $\Omega$ и $\Theta$-оценок, важно понимать, что алгоритм может работать по-разному в разных случаях в зависимости от инпута. Рассмотрим простую функцию поиска элемента в массиве:

1
2
3
4
5
6
7
8
int find_element(const vector<int>& a, int x) {
    for (int i = 0; i < a.size(); ++i) {
        if (a[i] == x) {
            return i;
        }
    }
    return -1;
}

В лучшем случае, когда элемент находится в начале массива, алгоритм сделает одно сравнение и вернет индекс. В худшем случае, когда элемента нет в массиве, алгоритм сделает $n$ сравнений. В среднем случае, когда элемент находится в массиве в случайном месте, алгоритм сделает $\frac{n}{2}$ сравнений.

По этой причине для некоторых алгоритмов мы будем говорить о времени работы в лучшем, худшем и среднем случае.