Мы уже рассмотрели несколько сортировок, которые работают за $O(n \log n)$, но что если мы хотим сортировать быстрее? Оказываеся, что при наличии некоторых естественных ограничений, можно доказать, что быстрее сортировать нельзя. То есть в этом разделе докажем нижнюю оценку на время работы сортировки.

Естественные ограничения

Мы введём следующие ограничения:

• С элементами массива можно производить только сравнения (за $O(1)$), то есть мы не можем применять арифметические, битовые и любые другие операции над элементами массива
• Сортировка принимает на вход массив из $n$ элементов и возвращает массив индексов в отсортированном порядке (перестановку)

Любая сортировка, которая удовлетворяет этим ограничениям, называется сортировкой сравнениями. Все рассмотренные ранее алгоритмы сортировки являются сортировками сравнениями (bubble, merge, quick sort).

Мы докажем только детерминированный вариант теоремы, для рандомизированных алгоритмов доказательство схоже и потребует лишь технического ввода меры над распределениями деревьев решений.

Доказательство

Худший случай

Докажем, что любая сортировка сравнениями работает за $\Omega(n \log n)$ в худшем случае. То есть для любого алгоритма сортировки сравнениями найдется такой входной массив, на котором время работы будет хотя бы $\Omega(n \log n)$.

Поскольку нам доступна только одна операция - операция сравнения - рассмотрим наш алгоритм как дерево решений. Дерево решений - это бинарное дерево, в котором каждая вершина соответствует одному сравнению, а в листьях дерева находятся перестановки элементов массива - результат работы функции.

Вот как выглядит дерево решений для сортировки массива из 3 элементов ($a$, $b$ и $c$):

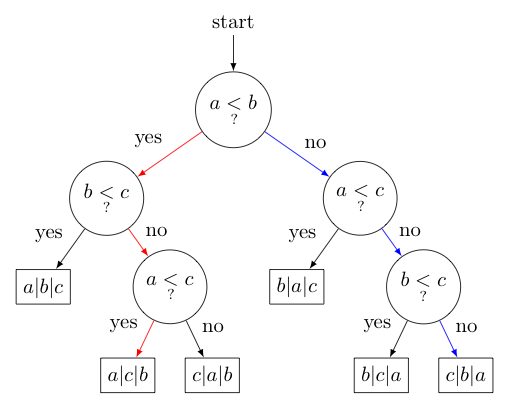
Заметим, что глубина дерева (то есть самый длинный путь от корня до листа) - это количество сравнений, которое делает наш алгоритм в худшем случае (для определения какой-то из перестановок). Мы должны показать, что глубина дерева не меньше $\Omega(n \log n)$.

Доказальство в три шага:

Шаг 1. Поскольку у нас есть $n!$ перестановок, то листьев у нашего дерева будет как минимум $n!$ - без этого мы не сможем различить как минимум две перестановки и следовательно выдадим неправильный ответ на одной из них.

Шаг 2. Поскольку у бинарного дерева глубина не меньше логарифма числа листьев, то получаем, что глубина дерева не меньше $\log_2 n!$.

Шаг 3. Оценим снизу $\log_2 n!$.

Оценка для студентов Стирлингом

По Формуле Стирлинга $\ln n! = n \ln n - n + O(\ln n) = \Omega(n \log n)$. Но на самом деле вы даже доказали точкую оценку с учетом константы!

Оценка для школьников неравествами

Обозначим за $k = \lfloor \log_2 n \rfloor$.

Тогда $\log n! = \log 1 + \log 2 + \log 3 + \log 4 + \log 5 + \ldots + \log (n - 1) + \log n \geq \ldots$

Оценим сверху каждое слагаемое ближайшей меньшей степенью двойки под логарифмом:

$\ldots \geq \log 1 + \log 2 + \log 2 + \log 4 + \log 4 + \ldots = 0 + 2 \cdot \log 2 + 4 \cdot \log 4 + 8 \log 8 + \ldots + 2^{k} \log 2^{k} \geq \ldots$

Оценим сумму как последнее слагаемое:

$\ldots \geq k^2 \log 2^{k} = \Omega(n \log n)$.

В итоге мы доказали, что $\log_2 n! = \Omega(n \log n)$, следовательно глубина дерева решений не меньше $\Omega(n \log n)$, что и требовалось доказать.

Средний случай

Докажем, что любая сортировка сравнениями работает за $\Omega(n \log n)$ в среднем.

Доказательство леммы

Очевидно. Переподвесим нижний лист к верхнему, уменьшив суммарную глубину. Если надо, то придется создать еще один лист, чтобы сохранить их количество в процессе переподвешивания.

По лемме средняя глубина листьев минимизируется на дереве, у которого минимальная и максимальная глубина листа отличается не больше чем на константу, то есть дерево “почти сбалансировано”, следовательно глубина каждого листа примерно равна, и равна примерно $\log n$ (меньше нельзя, чтобы было $n$ листьев).

Таким образом, минимальная средняя глубина листьев дерева решений с $n!$ листьями равна $\Omega(\log n!) = \Omega(n \log n)$.