Замечание мы везде будем использовать полуинтервалы $[l; r)$, поскольку обычно это избавляет от проблем с индексацией (не надо думать о $\pm 1$).

Префиксные суммы

Дан массив $a$ длины $n$. Нужно уметь отвечать на запросы суммы на отрезке - иначе говоря вычислять $a_l + a_{l + 1} + \ldots + a_r$ за $O(1)$ на запрос.

Для того, чтобы эффективно вычислять сумму на отрезке, мы можем использовать префиксные суммы. Префиксная сумма - это массив, в котором $i$-й элемент равен сумме первых $i$ элементов массива $a$. То есть:

Тогда сумма на отрезке $[l; r)$ будет равна:

Таким образом, мы построили простейшую структуру данных - один массив - за $O(n)$ времени предпросчета, заняли $O(n)$ дополнительной памяти и умеем отвечать на запросы за $O(1)$ времени.

Упражнение: научитесь находить прозведение на отрезке (не забудьте, что бывают нули!).

А что если мы захотим обновить массив?

Eсли мы захотим обновить элемент массива (иначе говоря добавить новый тип запроса - изменить элемент), то нам придется обновить все префиксные суммы, что займет $O(n)$ времени. Поэтому префиксные суммы не подходят для задач, где нужно обновлять массив.

Дерево отрезков

Дерево отрезков позволит нам обрабатывать запросы суммы на отрезке и обновления массива, но за это будет плата - $O(\log n)$ времени на запрос. И более того, как мы с вами поймем дальше, дерево отрезков позволит решить множество абсолютно разнообразных задач, которые с ходу могут показаться совершенно не связанными друг с другом!

Пусть массив $a = [13, -1, 2, 23, -4, 231, 13, 5, 2, -88, -52, 0, 4, 90, 3, -12]$ Дерево отрезков над массивом $a$ - это “рекурсивная” структура и выглядит следующим образом:

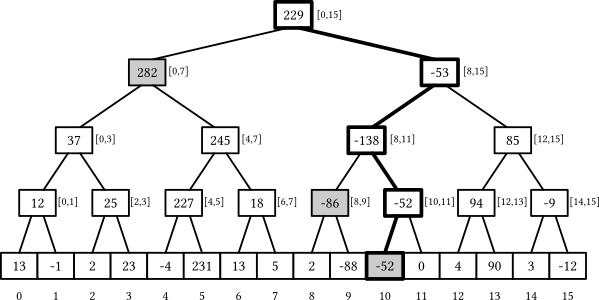
Каждая вершина дерева отрезков хранит некоторую информацию о массиве, а именно - сумму элементов массива на отрезке, который он описывает. Помимо этой информации каждая вершина хранит не больше двух детей - левого и правого. Левый ребенок описывает левую половину отрезка, а правый - правую. Таким образом, если мы знаем, что корень дерева описывает отрезок $[0; n)$, то его левый ребенок будет описывать отрезок $[0; n / 2)$, а правый - $[n / 2; n)$. И так далее.

Сколько уровней в дереве отрезков? А сколько памяти оно занимает?

Прежде чем переходить дальше, рекомендую подумать над этими вопросами масостоятельно.

Рассмотрим, как подобная, казалось бы, сложная структура поможет нам решить исходную задачу.

Построение дерева отрезков

Мы будем строить дерево отрезков рекурсивно. Если мы хотим построить дерево отрезков над массивом $a[l; r)$, то мы можем сделать это следующим образом:

1. Если $r - l == 1$, то мы находимся в листе дерева отрезков. В этом случае мы просто создаем вершину, которая хранит значение $a[l]$ и возвращаем ее.
2. Если $r - l > 1$, то мы находимся в внутренней вершине дерева отрезков. В этом случае мы можем разбить отрезок $[l; r)$ на два отрезка $[l; m)$ и $[m; r)$, где $m = (l + r) / 2$. Затем мы рекурсивно строим левое и правое поддеревья и создаем вершину, которая хранит сумму значений левого и правого поддерева.

Тогда реализация построения дерева отрезков будет очень простой:

1
2
3
4
5
6
7
8
9
10
11
12
13
int a[N]; // исходный массив
int t[2 * N]; // массив, в котором мы будем хранить дерево отрезков

int build(int v, int l, int r) { // в какой вершине находимся и за какой подобрезок она отвечает
    if (r - l == 1) { // если мы находимся в листе
        return t[v] = a[l]; // то просто записываем значение
    } else {
        int m = (l + r) / 2; // находим середину
        return t[v] = build(left(v), l, m) + build(right(v), m, r); // рекурсивно строим левое и правое поддеревья
    }
}

build(0, 0, n); // строим дерево отрезков над массивом a

О том, что такое left(v) и right(v) мы поговорим чуть позже.

Запрос обновления

Заметим, что лишь логарифм вершин дерева отрезков содержит информацию о значении $i$-го элемента массива. То есть нам нужно обновить в точности $\log n$ вершин при изменении одного элемента массива, и это крайне легко делать снизу вверх - сначала обновить лист, содержащий сумму только одного элемента ($a_{pos}$), затем его родителя, затем родителя родителя и так далее. Визуализировать обновление $a_2 = 7$ для массива $[5, 3, 1, 2, 8, 6, 4, 0]$ можно так:

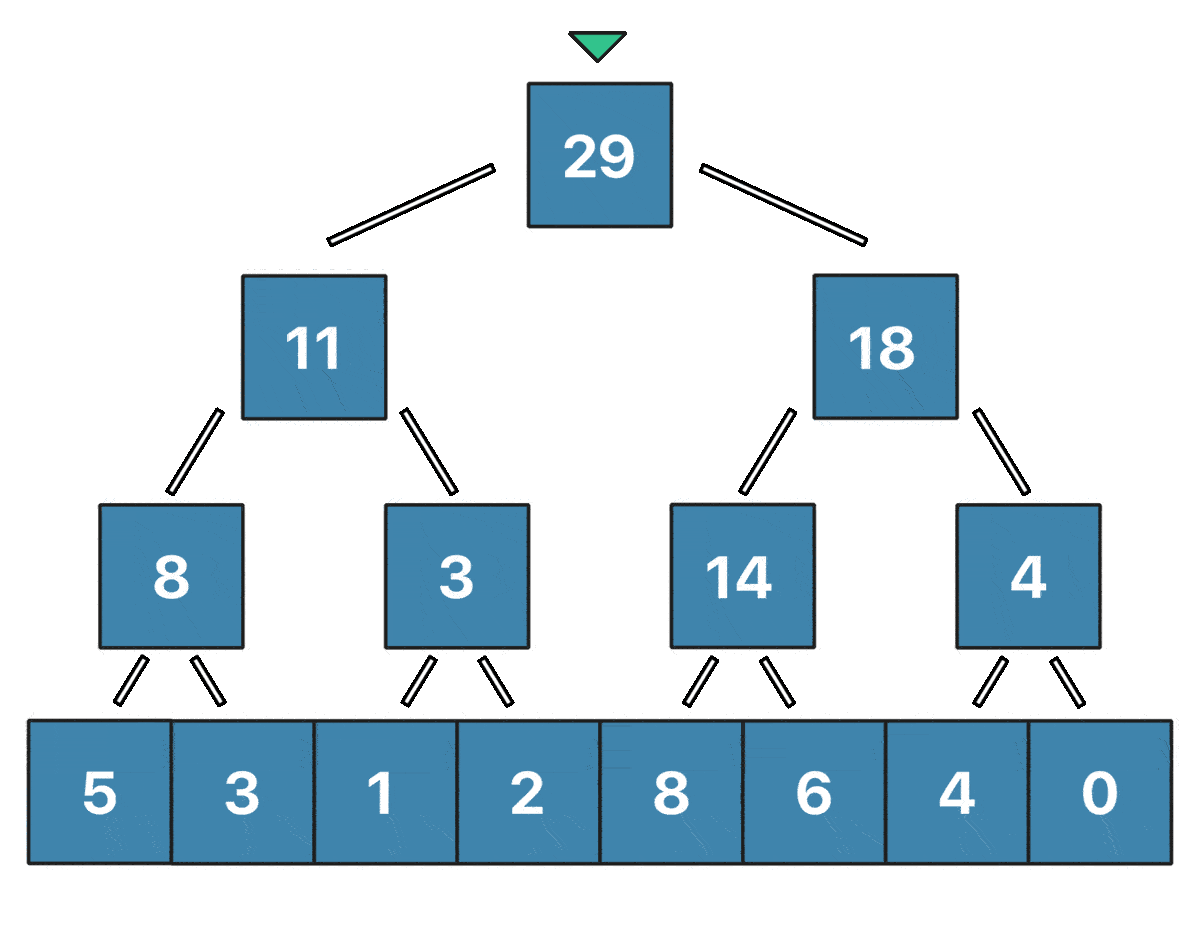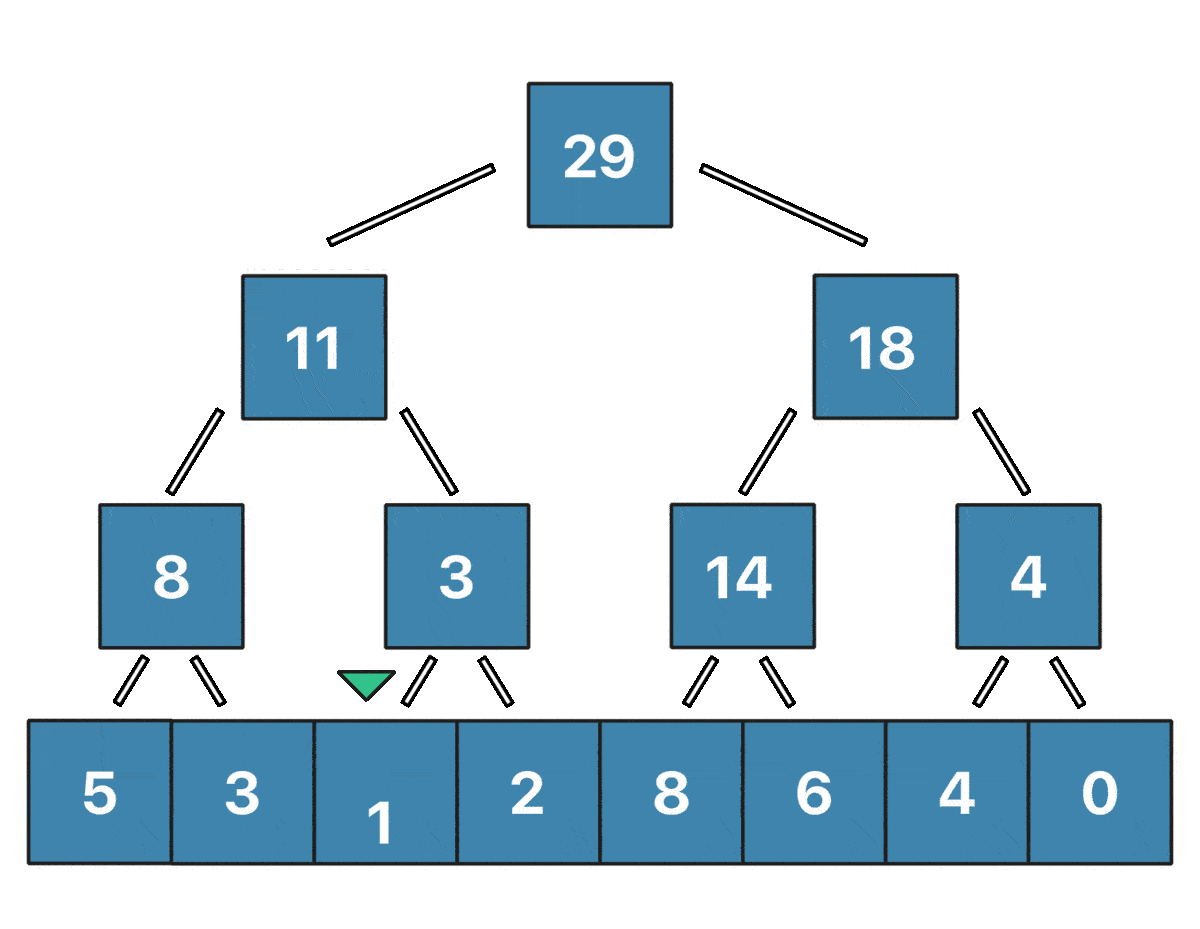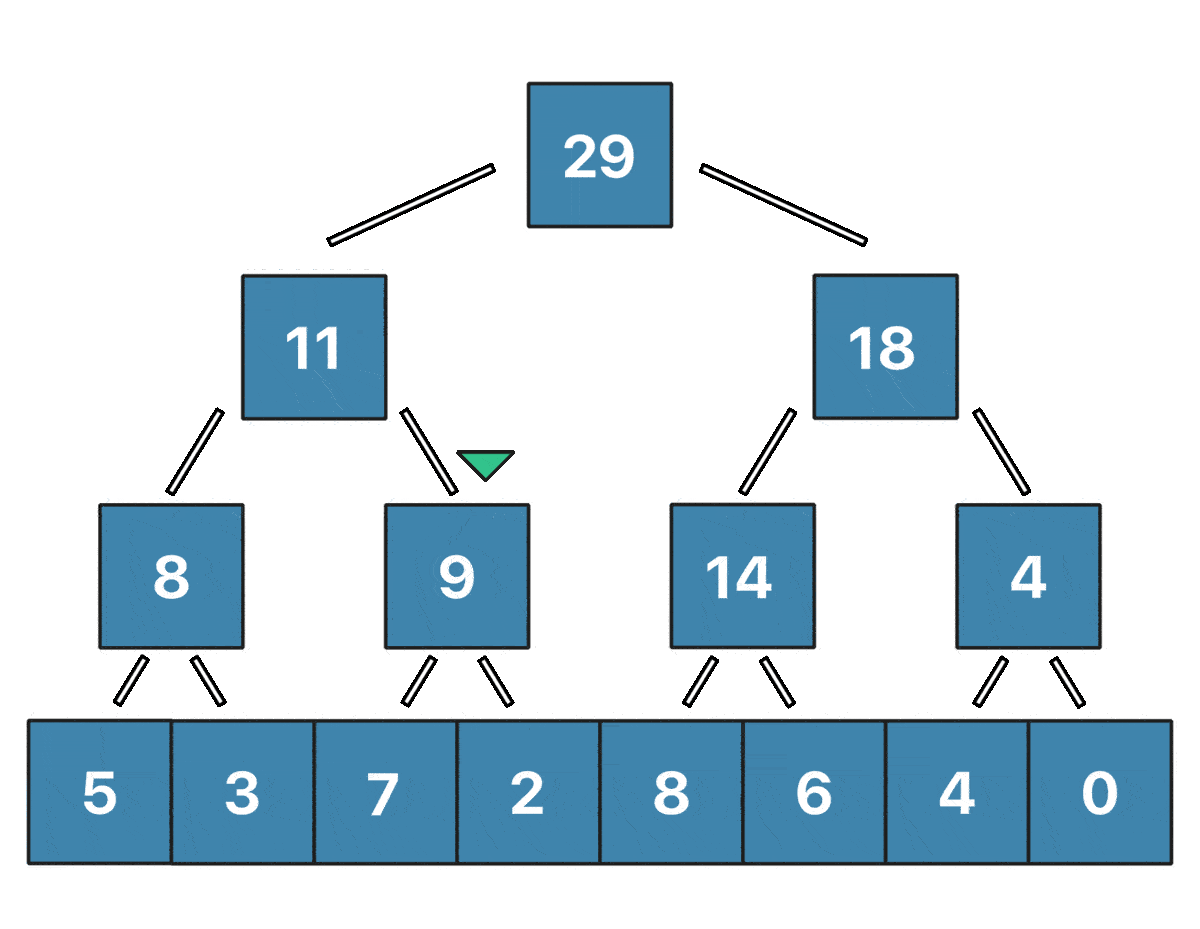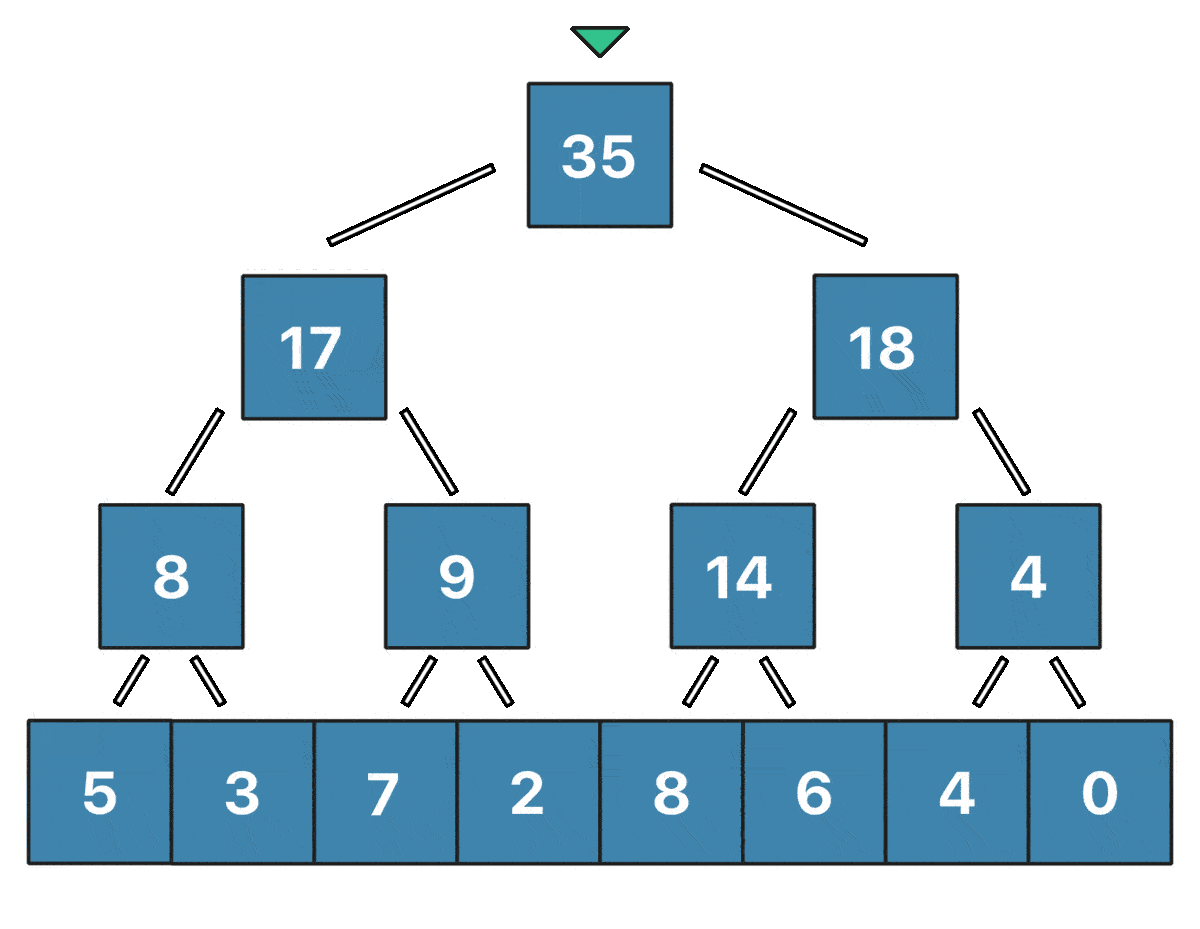
Реализация:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void update(int v, int l, int r, int pos, int x) // обновляем элемент pos на x; v - текущая вершина, в которой находимся, [l; r) - отрезок, который она описывает
{
    if (r - l == 1) { // если мы находимся в листе
        return t[v] = x; // то просто записываем значение
    } else {
        int m = (l + r) / 2; // находим середину
        if (pos < m) { // если pos находится в левой половине
            update(left(v), l, m, pos, x); // обновляем левое поддерево
        } else { // иначе pos находится в правой половине
            update(right(v), m, r, pos, x); // обновляем правое поддерево
        }
        t[v] = t[left(v)] + t[right(v)]; // обновляем значение в текущей вершине
    }
}

Запрос суммы

Остался самый “сложный” запрос - запрос суммы на отрезке $[ql; qr)$. О вычислении суммы на таком отрезке можно думать как об оптимизированном обходе всего дерева отрезков. Оптимизирован он будет потому, что мы не будем посещать заведомо “бесполезные” вершины. Рассмотим произвольную вершину $v$ ДО, которая отвечает за отрезок $[l; r)$ и отрезок $[ql; qr)$, сумму на котором мы хотим найти. Мы можем рассмотреть три случая:

1. Если отрезок $[l; r)$ не пересекается с отрезком $[ql; qr)$, то мы возвращаем 0 - такая вершина не вносит вклад в сумму, как и все её дети.
2. Если отрезок $[ql; qr)$ полностью содержит отрезок $[l; r)$, то мы возвращаем сумму на отрезке $[l; r)$ - такая вершина полностью входит в искомый отрезок, как и все её дети.
3. Если отрезок $[ql; qr)$ как-то иначе пересекает отрезок $[l; r)$, то мы рекурсивно ищем сумму в левом и правом поддеревьях.

Пример запроса суммы на отрезке $[2; 6)$ для массива $[5, 3, 1, 2, 8, 6, 4, 0]$:

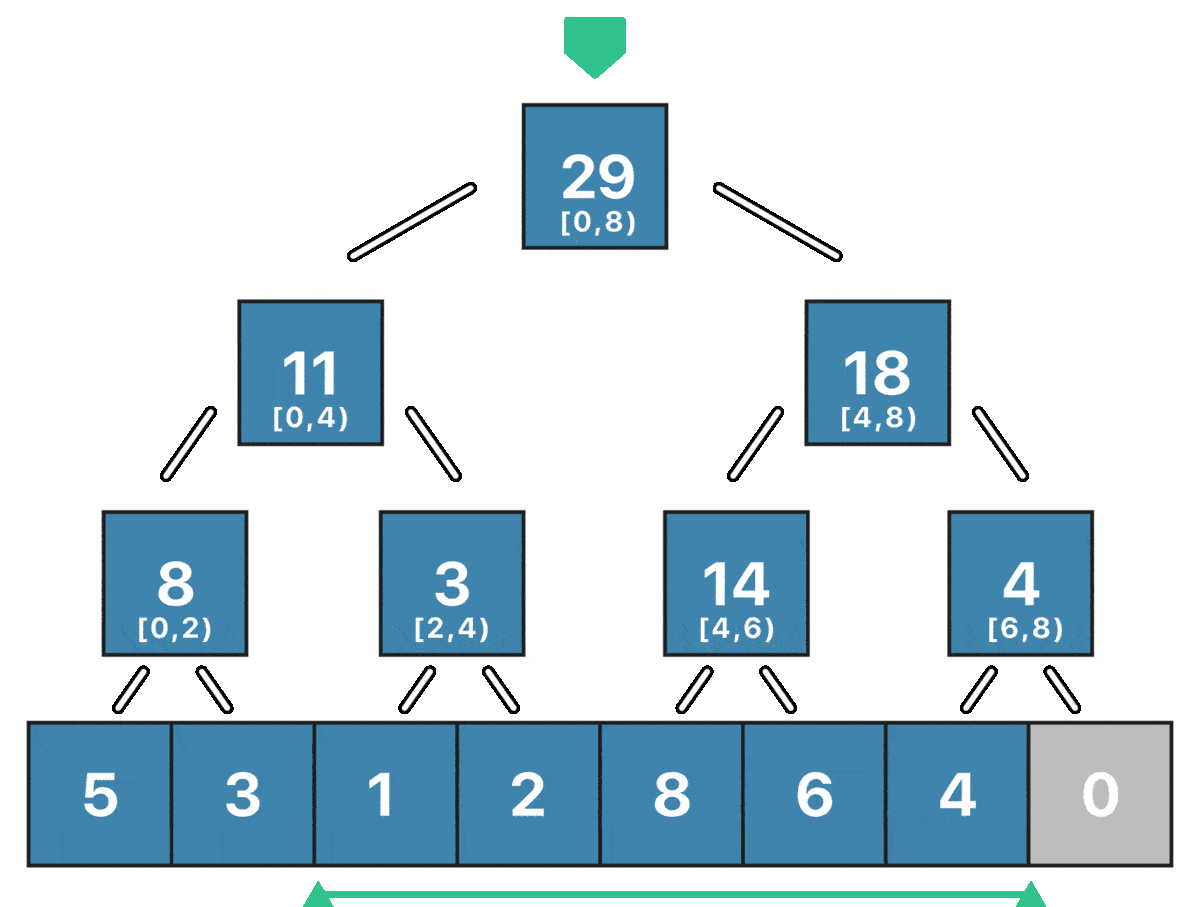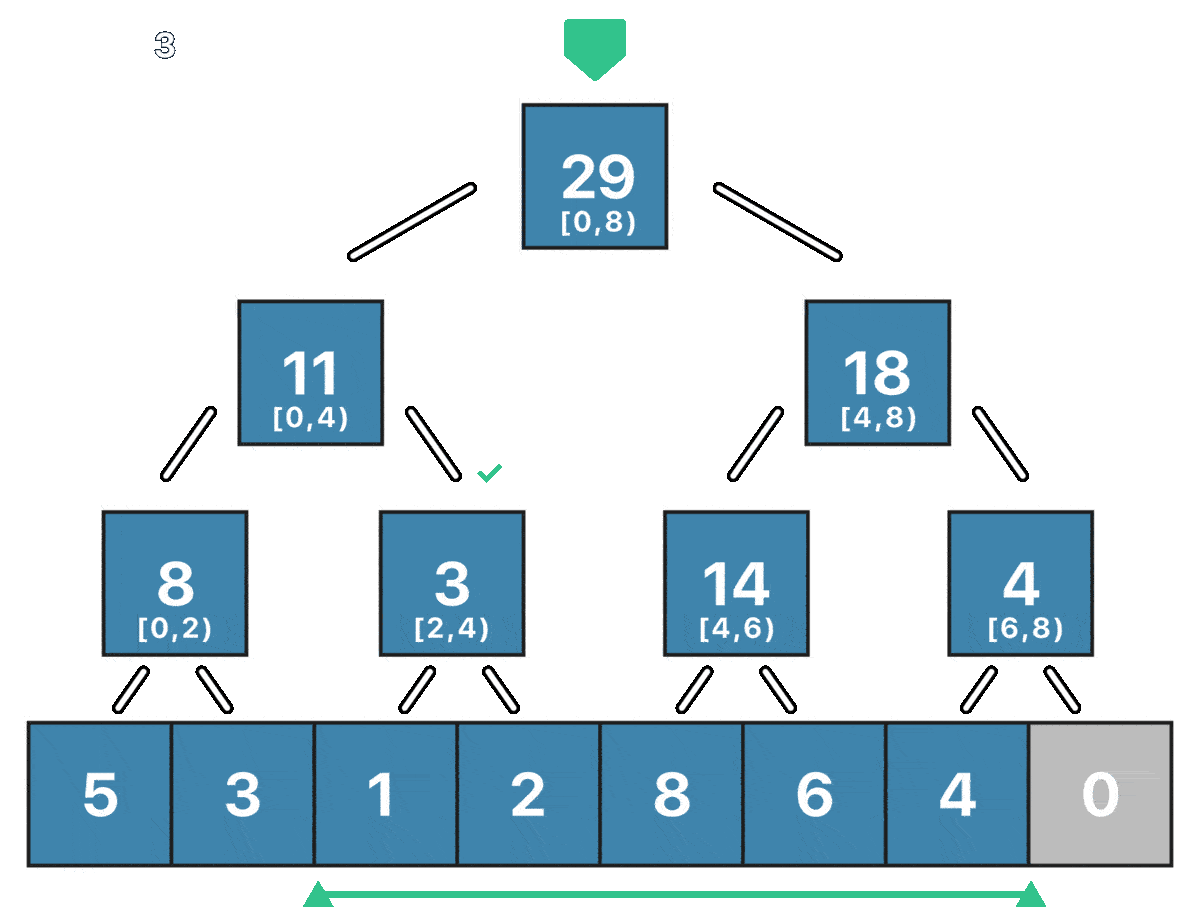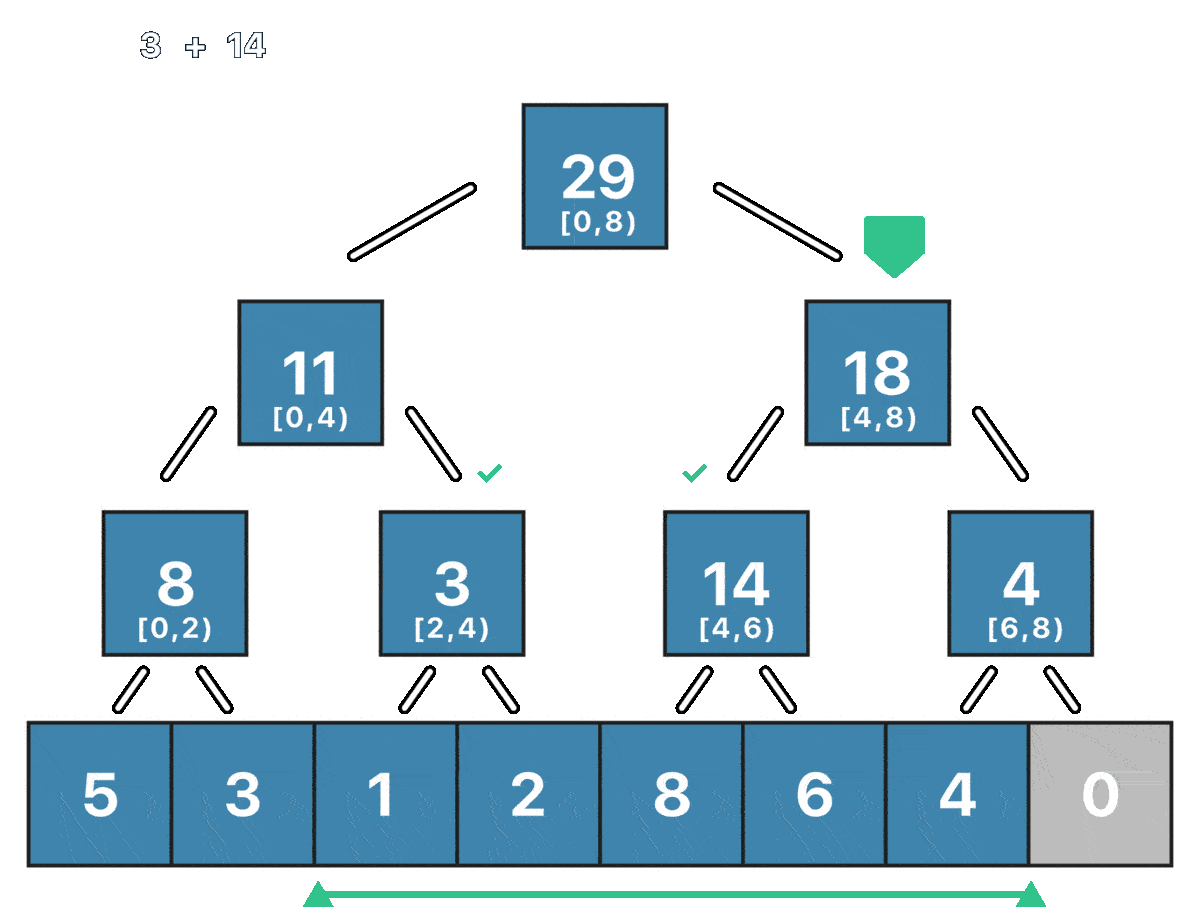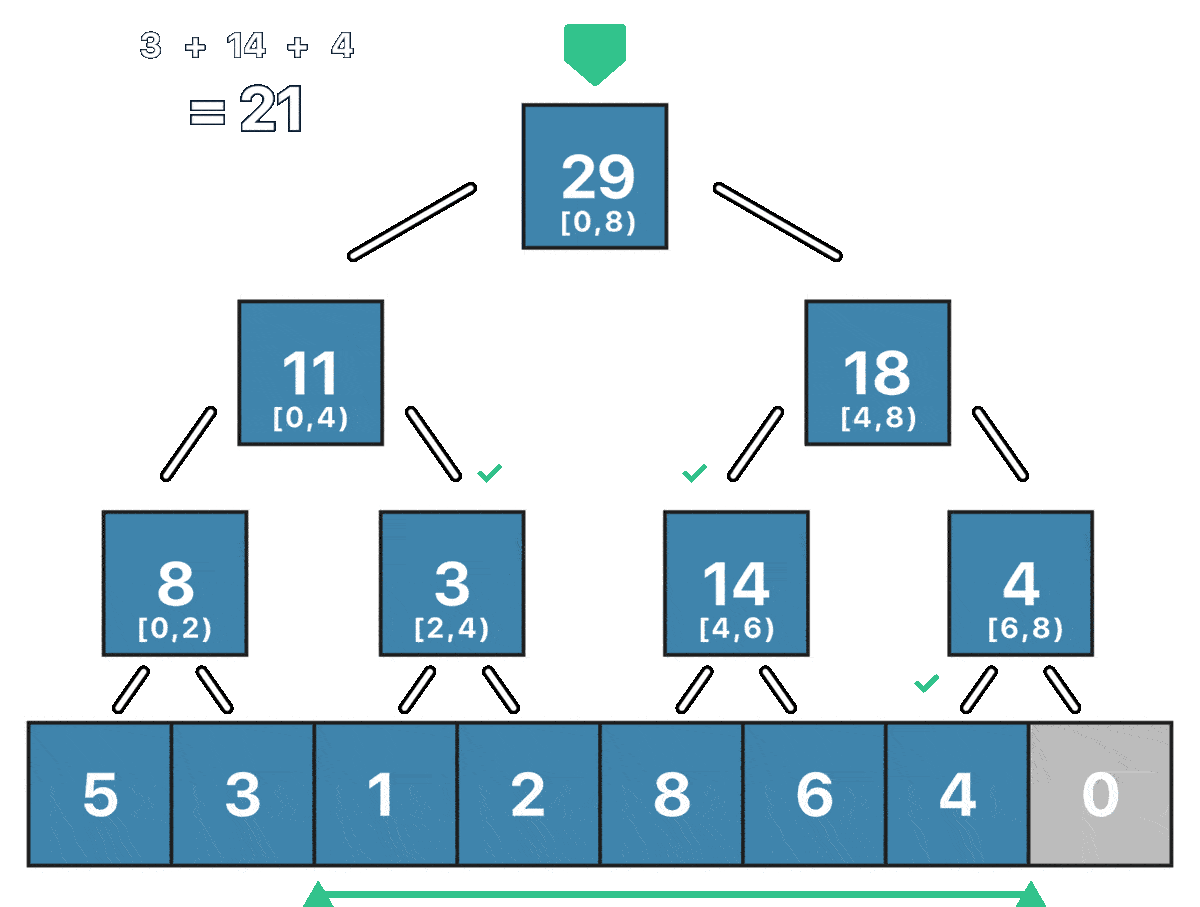
1
2
3
4
5
6
7
8
9
10
int sum(int v, int l, int r, int ql, int qr) { // надо найти сумму на отрезке [ql; qr), находимся в вершине v, которая отвечает за отрезок [l; r)
    if (ql >= r || qr <= l) { // если отрезок [ql; qr) не пересекается с отрезком [l; r), то возвращаем 0
        return 0;
    } else if (ql <= l && qr >= r) { // если отрезок [ql; qr) полностью содержит отрезок [l; r), то возвращаем сумму
        return t[v];
    } else { // иначе отрезок [ql; qr) пересекает отрезок [l; r), то рекурсивно ищем сумму в левом и правом поддеревьях
        int m = (l + r) / 2;
        return sum(left(v), l, m, ql, qr) + sum(right(v), m, r, ql, qr);
    }
}

Почему же такая оптимизация гарантирует $O(\log n)$ на запрос? Оказывается, это следует из двух фактов:

1. Глубина дерева отрезков $O(\log n)$.
2. Рекурсивный обход дерева отрезов будет посещать на каждом уровне не более $4$ вершин

Что такое left(v) и right(v)?

Вместо того, чтобы как-то явно хранить левого и правого ребенка в динамической памяти (что замедлит работу программы), мы будем хранить все вершины дерева отрезков в одном массиве. Однако наша задача будет понять: как имея номер вершины $v$ в массиве, найти номера ее детей. Для этого посмотриите внимательно на то, как будет устроена нумерация вершин, если их естественным образом пронумеровать сверху вниз и слева направо (синим цветом - номер вершины):

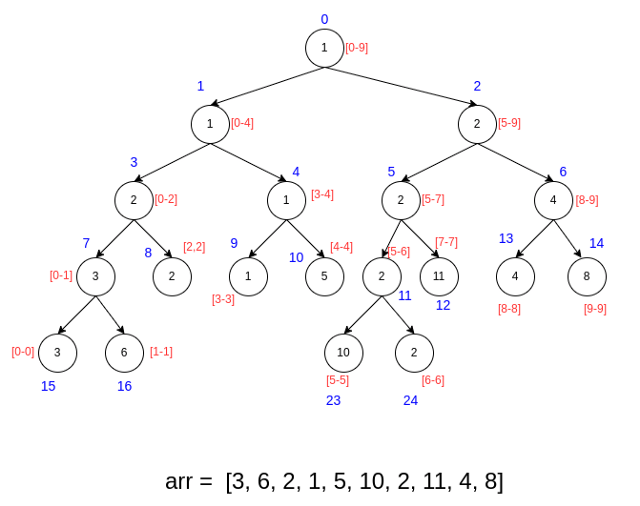
Легко заметить, что левый ребенок вершины $v$ будет находиться в позиции $2 * v + 1$, а правый - в позиции $2 * v + 2$. Таким образом, мы можем легко вычислить номера детей вершины $v$.

В С++ из языка С пришли макросы - это простейшие шаблоны, которые тоже разворачиваются на этапе компиляции:

1
2
#define left(v) (2 * (v) + 1)
#define right(v) (2 * (v) + 2)

Однако макросы разворачиваются “совсем глупо” - просто полностью копируя аргумент как текст (без вычисления выражения). Поэтому порядок арифметических действий в может быть нарушен - поэтому всё максимально обернуто в скобки. Простой пример, в котором порядок действий был сломался без скобок следующий:

1
2
3
4
#define bad_left(v) (2 * v + 1)

bad_left(1 + 2) // 2 * 1 + 2 + 1 = 5
// хотя вы бы ожидали 2 * (1 + 2) + 1 = 7

Упражнение: придумайте аргумент, при котором отсутсвие вншесних скобокn тоже приведет к ошибке.

Какие операции вообще можно поддерживать?

На самом деле дерево отрезков прекрасно справляется с операциями, которые можно “склеивать”: если мы знаем $f(l, m)$ и $f(m, r)$, то мы можем вычислить $f(l, r)$ за $O(немного)$ времени. К таким операциям относятся сумма, минимум, НОД и множество других операций. А вот, например, операция “количество различных чисел на отрезке” не является такой операцией.

Список задач

1. Необходимо научиться отвечать на два типа запросов: add $l$ $r$ $x$ - добавить на отрезке $[l; r)$ число $x$ и get $pos$ - узнать значение на позиции $pos$.
2. Необходимо научиться проверять, является ли подстрока $s_{l\ldots r}$ правильной скобочной за $O(\log n)$, строка состоит только из одного вида скобок - ().
3. Hа кольцевой парковке есть $n$ мест пронумерованых от $1$ до $n$. Есть два вида событий прибытие машину на парковку и отъезд машины с парковки. Если машина приезжает на парковку, а её место занято, то она едет далее по кругу и встаёт на первое свободное место.
4. Необходимо научиться искать $k$-ю порядковую статистику на отрезке за:
   1. $O(\log^3 n)$
   2. $O(\log^2 n)$
   3. $^{(*)}$ $O(\log n)$
5. $^{(**)}$ Необходимо научиться находить количество различных чисел на отрезке за $O(\log n)$.