В этом разделе мы научимся делать список частично персистентным за $O(1)$. Определим типы запросов, которые мы сможем поддерживать:

• AddAfter(u, x) - вставить новую вершину x после вершины u
• Delete(u) - удалить вершину u
• Next/Prev(u_k) - получить следующую/предыдущую вершину в списке от вершины u (зная, что она версии k)
• Конечно в каждой вершине можно хранить дополнительную информацию, но нас это не интересует.

Для простоты мы разберем только запрос добавления, а удаление будет аналогично.

Проблема

Предположим, что мы захотим воспользоваться методом fat node, аналогично персистентному массиву. Тогда в каждой вершине нам нужно будет хранить список указателей на все следующие и предыдущие вершины всех версий.

1
2
3
4
5
6
7
8
9
10
11
struct Neighbor {
    int version;
    Node *ptr;
}

struct Node {
    vector<Neighbor> next;
    vector<Neighbor> prev;
    // maybe some additional information and its versions
    // ...
}

Такой подход сделает структру персистентной, но запрос Next/Prev будет работать за $O(\log n)$ из-за бинпоиска нужной версии.

Решение

Ограничим список из next/prev всего лишь двумя версиями.

1
2
3
4
struct Node {
    optional<Neighbor> next[2];
    optional<Neighbor> prev[2];
}

Главный вопрос - что делать, если на шаге $k$ у нас уже есть две заполненные версии next у вершины $u$, и мы хотим добавить новую вершину $v$ после $u$? В таком случае мы будем применять технику copy path:

• Если $u$ уже имеет две версии next, то мы создаем новую вершину $u’$, соединяя ее с $prev(u)$ и $v$.
• Если $prev(u)$ тоже имел две версии next, то придется проделать такую же процедуру копирования, пока не дойдем до вершины, у которой есть свободная версия next.
• Аналогично делаем и для вершины $next(u)$, предком которой теперь будет $v$.

Рассмотрим на примере: пусть есть список из 5 вершин версии $V_0$ (черный):

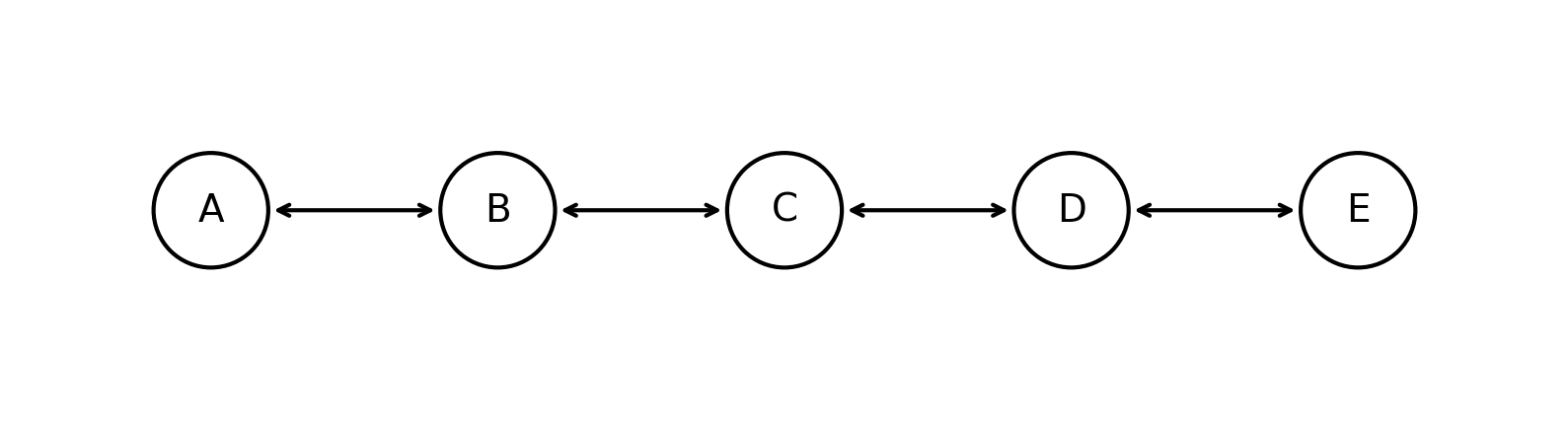
Теперь персистентно добавим вершину $F$ между $B$ и $C$, поскольку у каждой из них занят только один next/prev, то мы лишь добавим указатели на $F$ в $B$ и $C$:

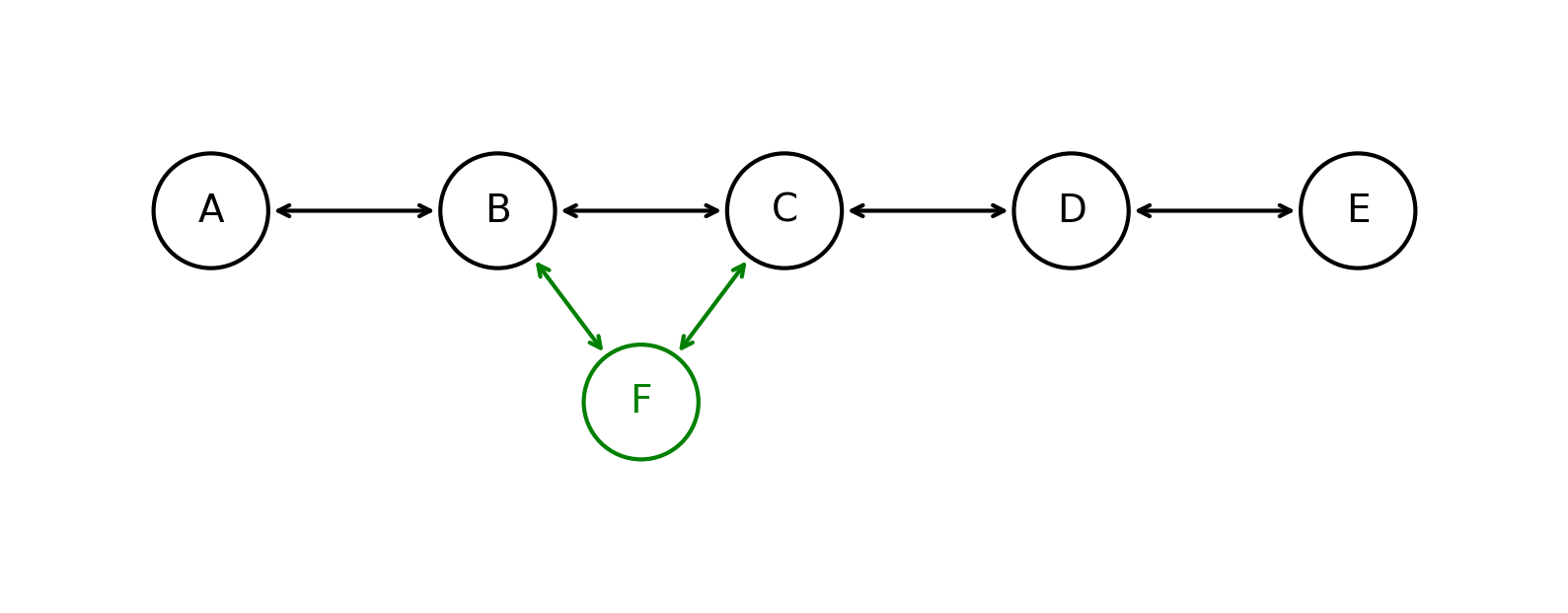
Теперь добавим вершину $G$ между $C$ и $D$. Опять же у $C$ и $D$ только по одному next, поэтому мы просто добавим указатели на $G$ в $C$ и $D$:

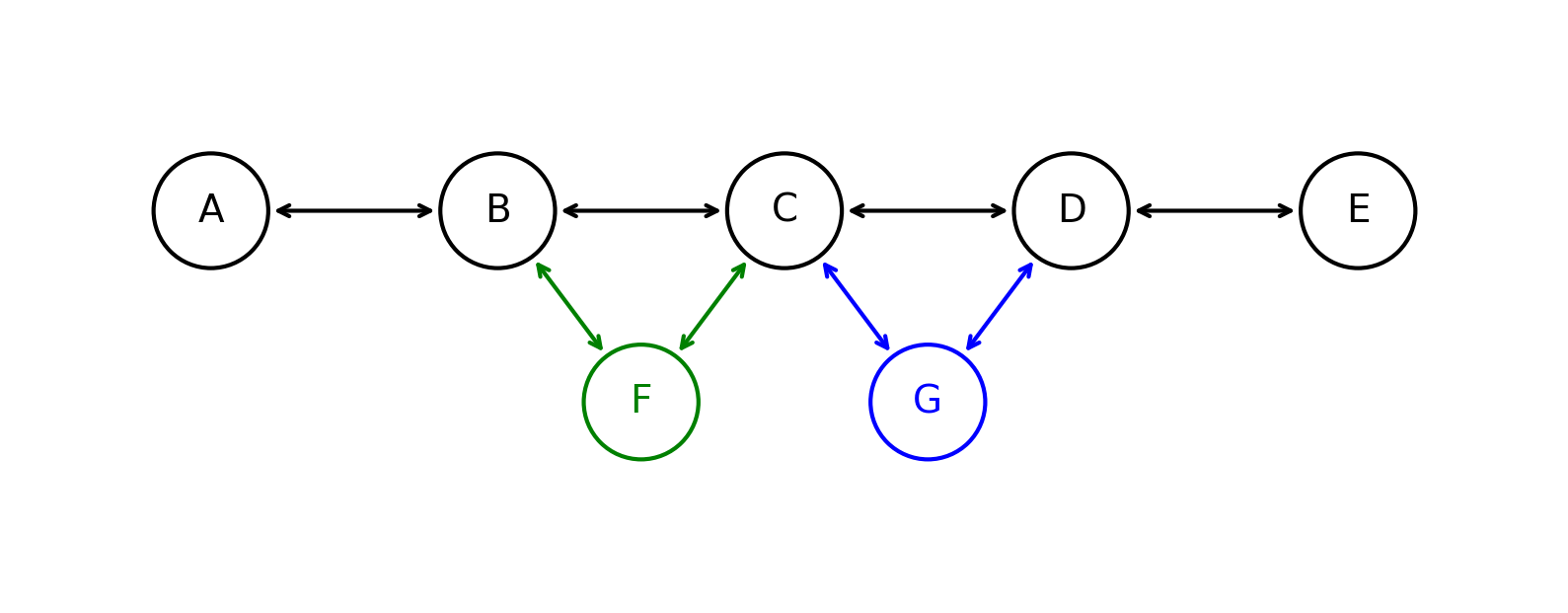
Теперь добавим вершину $H$ между $F$ и $G$. У каждой из них опять же есть один свободный next/prev, поэтому мы просто добавим указатели на $H$ в $F$ и $G$:

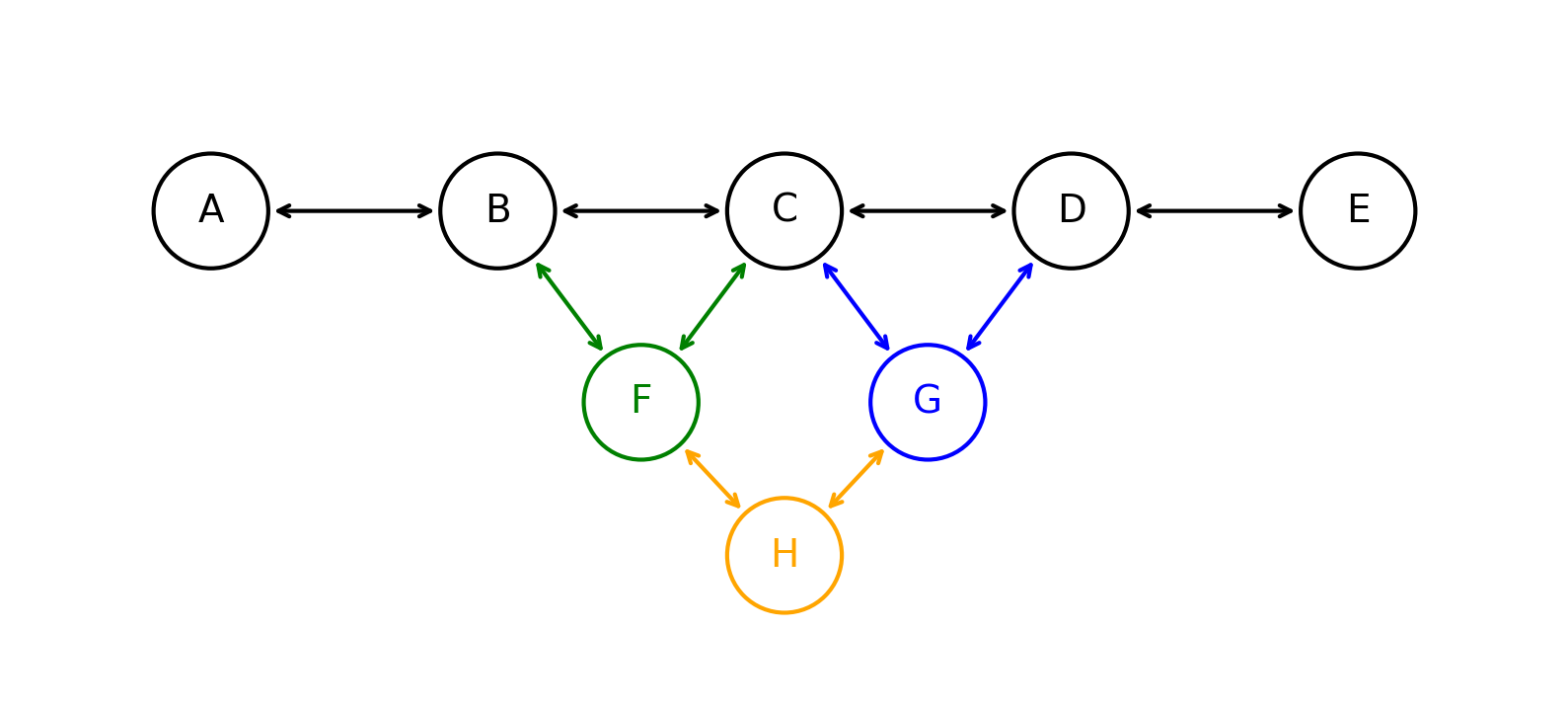
Наконец, добавим вершину $K$ между $B$ и $F$, тогда у $B$ и $F$ уже есть по два занятых next/prev, поэтому нам придется создать новую вершину $B’$, аналогично будет для почти всех вершин за исключением $A$ и $E$ (у них по одному занятому next/prev):

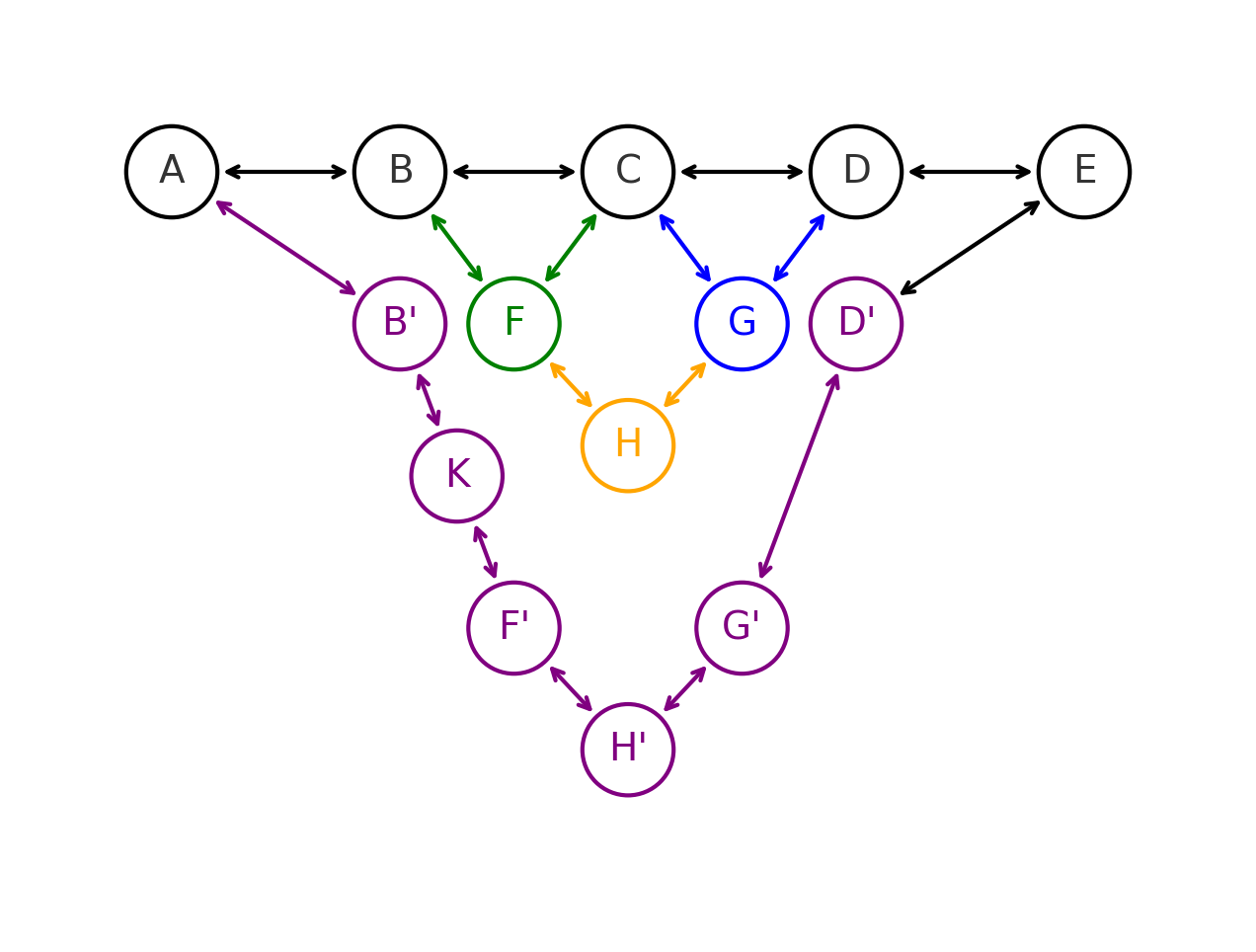
Анализ времени работы

Утверждается, что такая структура будет работать за $O(1)$ в среднем. Для доказательства воспользуемся банковским методом:

• В каждой вершине при переходе из $1$ занятого next в $2$ занятых next мы добавляем $1$ монетку в вершину. В таком случае в алгоритме не происходит копирований, поскольку у вершины хватает свободной версии next.
• Если мы копируем вершину, то мы платим $1$ монетку из вершины, которую ранее мы гарантированно имели, поскольку она обязана была перейти из $1$ занятого next в $2$ занятых next. А больше вершину копировать из-за переполнения next не придется.
• Аналогично для prev.

Таким образом баланс всегда неотрицательный и на каждом шаге мы добавляли не больше $2$ монетки в вершину, а значит мы можем гарантировать $O(1)$ в среднем.