Свойства

Фильтр Блума - это структура данных, которая позволяет проверять, принадлежит ли элемент множеству или нет за $O(1)$ в ХУДШЕМ случае с возможностью вставки и удаления. Однако в отличии от хеш-таблиц он не будет гарантировать 100%-ную точность.

Чуть более подробно - фильтр будет гаратнтировать, что если элемент принадлежит множеству, то структура гарантированно вернет true, а если не принадлежит, то с некоторой вероятностью ошибется.

Другой важной особенностью является то, что фильтр Блума не будет явно хранить элементы, то есть какими бы тяжелыми не были элементы, вы всегда будете тратить только $O(1)$ памяти вместо их реального размера!

Практика

С учетом всех замечательных свойств фильтра Блума, он массово применяется в реальных задачах. Например, он используется в поисковых системах для проверки, есть ли страница в индексе или нет: сначала запрос идет в фильтр Блума и только если он вернет true, то запрос идет в хеш-таблицу, которая хранит все страницы.

Также фильтр Блума используется в системах контроля версий, например, в Git, для проверки, есть ли файл в репозитории или нет. Кроме того, фильтр Блума используется в системах распределенного хранения данных, например, в Apache Cassandra и Amazon DynamoDB, для проверки, есть ли данные в кластере или нет.

Устройство

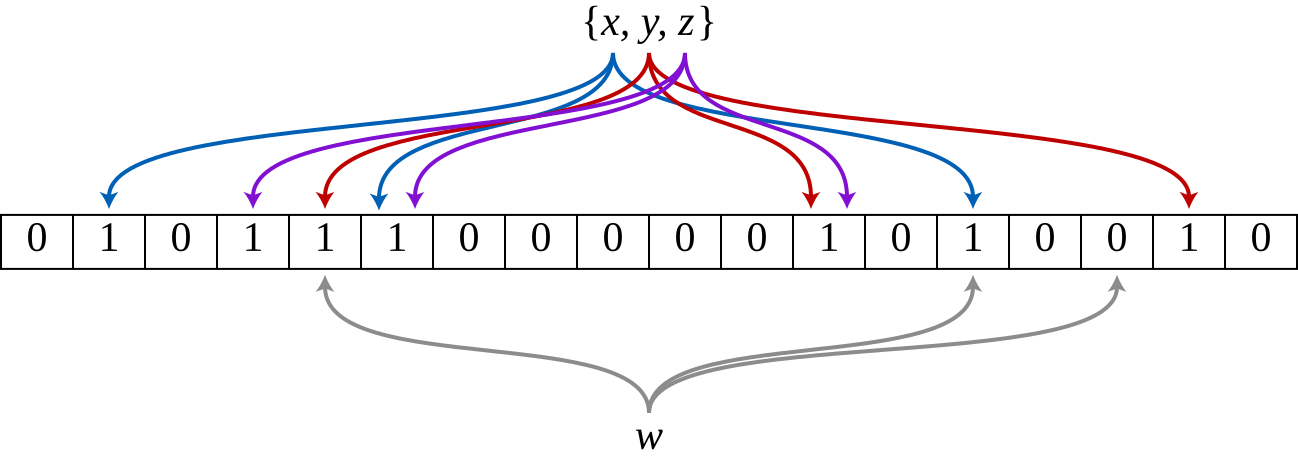
Фильтр Блума состоит из массива битов заранее фиксированного размера $M$ и $k$ хеш-функций, которые отображают элементы в диапазон от $0$ до $M-1$.

• При вставке элемента мы вычисляем $k$ хешей для него и устанавливаем соответствующие биты в массиве в 1.
• При проверке принадлежности элемента множеству мы вычисляем $k$ хешей для него и проверяем, установлены ли соответствующие биты в массиве в 1. Если все биты установлены, то считаем, что элемент принадлежит множеству, иначе - не принадлежит.

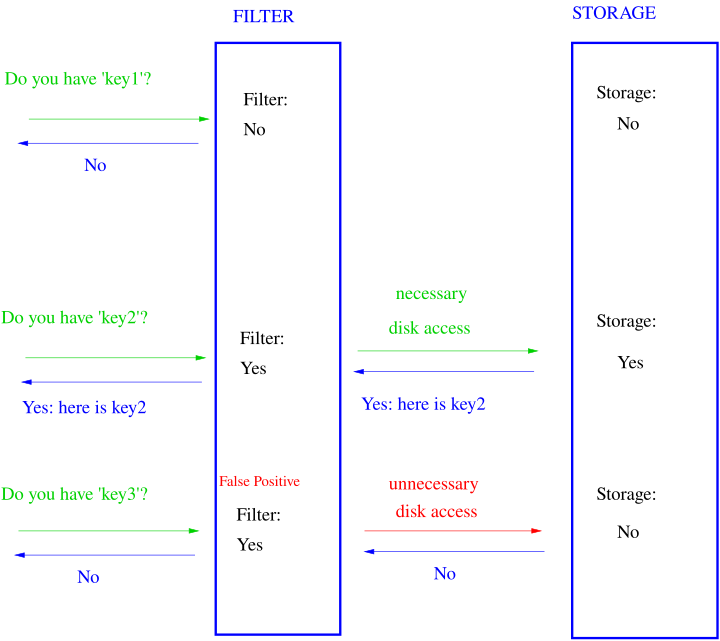
Как мы видим из схемы, фильтр Блума действительно может иметь только ложноположительные ошибки, но не может иметь ложноотрицательных.

Упраженение: а как поддерживать удаления из фильтра Блума?

Вероятность ошибки

Структура данных удивительно проста, но какая же вероятность ложноположительного срабатывания?

Пусть $N$ - количество элементов в фильтре, $M$ - размер массива битов, $k$ - количество хеш-функций. Предположим, что что хеш-функции равеномерно случайно выдают числа от $0$ до $M-1$, то есть:

\[P[h_i(x) = t] = \frac{1}{M}\]

Тогда вероятность того, что $t$-й бит не уставлен в 1 при вставке одного элемента будет равна:

\[P[h_1(x) \neq t, \ldots, h_k(x) \neq t] = \left(1 - \frac{1}{M}\right)^k\]

А вероятность того, что $t$-й бит не уставлен в 1 при вставке всех $N$ элементов будет равна:

\[P[\forall x \in A: h_1(x) \neq t, \ldots, h_k(x) \neq t] = \left(1 - \frac{1}{M}\right)^{kN}\]

Что при достаточно большом $M$ по второму замечательному пределу примеро равно:

\[P[\forall x \in A: h_1(x) \neq t, \ldots, h_k(x) \neq t] \approx e^{-\frac{kN}{M}}\]

Ложноположительное срабатывание будет происходить, если все $k$ бит установлены в 1, то есть с вероятностью:

\[P[\text{false positive}] \approx \left(1 - e^{-\frac{kN}{M}}\right)^k\]

Мы можем оптимизировать данную формулу по $k$, найдя оптимальное количество хеш-функций:

\[k = \frac{M}{N} \ln 2\]

Тогда сама вероятность ложноположительного срабатывания будет равна:

\[P[\text{false positive}] \approx 0.61^{\frac{M}{N}}\]

То есть уже при $M=10N$, что соответствует 10 битам на каждый элемент, вероятность ложноположительного срабатывания будет равна $0.61^{10} \approx 0.007$, что уже очень сильно!

Ссылки

1. Фильтр Блума на Wikipedia