Задача

В RAM-модели переставить элементы в массиве (англ. permutation problem) - это простейшая задача, в которой нужно по заданному массиву $a_n$ и перестановке $\pi(n)$ построить массив $b_k = a_{\pi(k)}$. Такая задача решается за $O(n)$ в RAM-модели, однако в модели внешней памяти (EM модель) мы получим более эффективный алгоритм и даже докажем его оптимальность по модулю некоторых предположений.

Что такое indivisibility assumption?

Indivisibility assumption - это по сути другая модель внешней памяти, которая с одной стороны крайне похожа на EM модель, но с другой - имеет несколько ключевых различий. В Indivisibility Model мы будем иметь всё те же три параметра $M$, $N$ и $B$, однако набор операций чуть-чуть отличается:

• $Read(e, B)$ - это операция чтения блока данных из внешней памяти в котором содержится элемент $e$
• $Write(e, B)$ - это операция записи блока данных во внешнюю память, в котором содержится элемент $e$
• Все операции над элементами в RAM неизменяемые (atomic) и выполняются за $O(1)$, то есть вы не можете менять элементы из инпута - они являются “неделимыми” единицами информации.
• Для простоты анализа мы будем разрешать оперировать только целиком блоками размера $B$

С одной стороны данная модель сильнее, чем EM модель, поскольку она умеет волшебным образом доставать нужный вам элемент из произвольного места во внешней памяти без полного ее сканирования. С другой стороны она слабее, поскольку не позволяет вам делать произвольные операции над элементами массива, а только операции чтения и записи.

Для наглядности понимания того, как соотносятся EM модель и Indivisibility модель предлагаю сузить EM модель до EM atomic model - EM модели, в которой нельзя выполнять произвольные операции над элементами. В таком случае легко осознать, что мы получили пересечение EM модели и Indivisibility модели. Кроме того, можно легко представить EM comparison model - это почти EM atomic model, но с дополнительно операцией сравнения двух элементов (она пригодится нам дальше для доказательства оптимальности сортировки). Диаграма доступных операций в разных моделях будет выглядеть следующим образом:

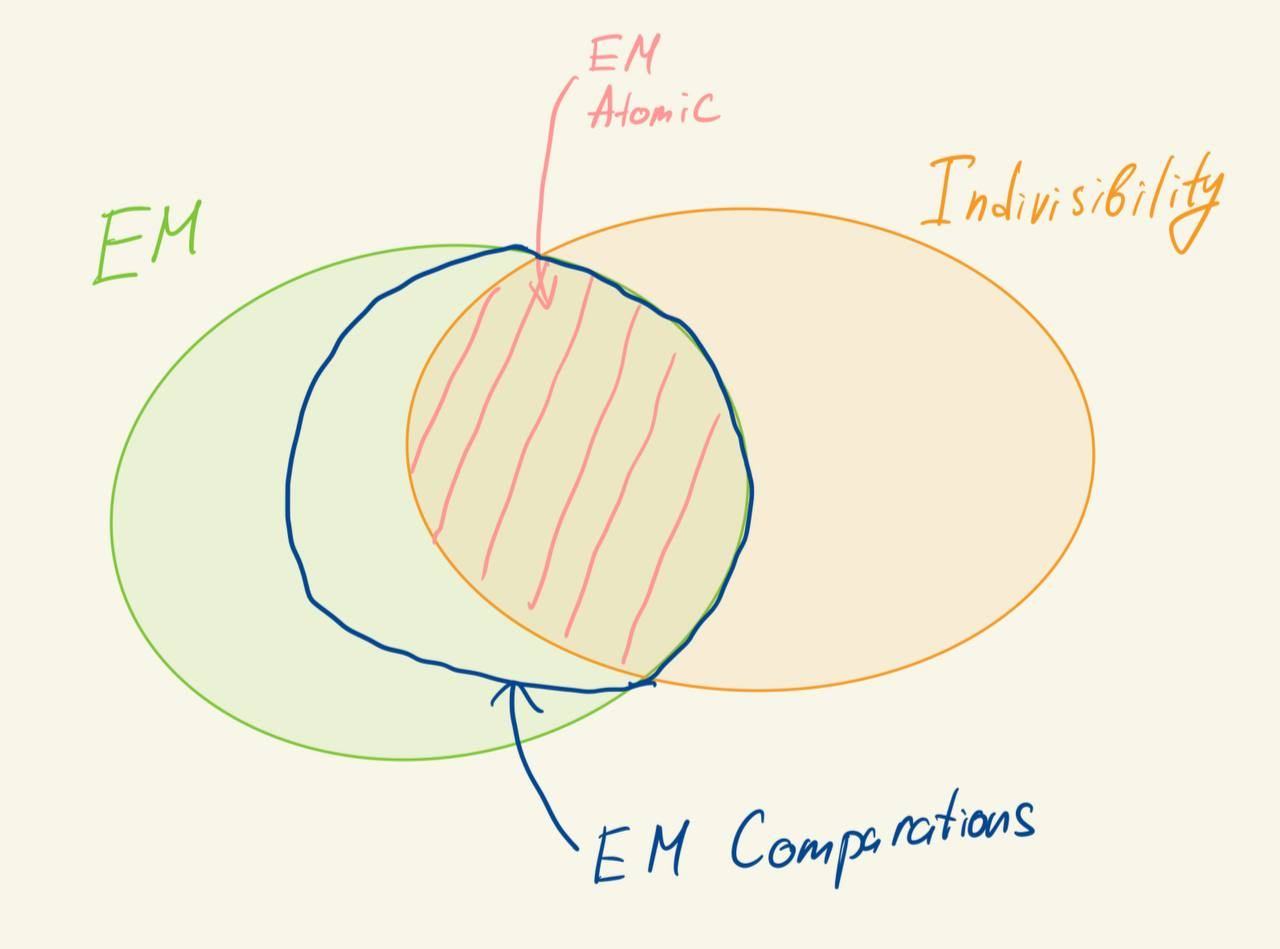
Indivisibility assumption - удобная модель для нижней оценки времени работы алгоритма, которая позволяет нам не задуматься о том, какие операции доступны над элементами массива. В общем случае для EM модели до сих пор не существует хорошей нижней оценки на время работы алгоритма перестановки.

Доказательство

Построение алгоритма

Есть два простейших алгоритма, которые решают эту задачу: мы можем в лоб, как в RAM-модели, пройтись по массиву и записать элементы в нужные места, это будет случай с $O(n)$ оценкой. Второй случай - это отсортировать массив пар $(\pi(i), a_i)$, что займет $O(\frac{N}{B} \log_{\frac{M}{B}} \frac{N}{B})$, таким образом мы получим верхнюю оценку на время работы алгоритма как минимум из двух алгоритмов. Важно заметить, что оба алгоритма удовлетворяют indivisibility assumption.

Оптимальность

Шаг 1. Зафиксируем произвольный алгоритм перестановки, пусть в худшем случае для какой-то фиксированной перестановки он совершил $H$ операций чтения и записи. Далее мы можем рассматривать лишь алгоритмы с $H \leq n^2$, в противном случае нижняя оценка уже $\Omega(n^2)$, которая сильнее той, что мы хотим доказать.

Шаг 2. Будем думать о блоке длины $B$ как о неупорядоченном (мульти)множестве, поскольку за 1 операцию мы можем загрузить его во внутреннюю память и расставить в произвольном порядке. Поэтому мы будем называть блок использованным, если блок, как неупорядоченное множество, уже передавался из внешней памяти во внутреннюю или наоборот.

Шаг 3. Определим состояние алгоритма, как набор некоторых мультимножеств: первое мультимножество - это вся внутянняя память (поскольку мы мы можем ее упорядочить как нам вздумается), после него будут идти все когда-либо использованные блоки в течение работы алгоритма (правда эти блоки мы можем менять операцией вывода).

Шаг 4. По определению $H$ количество мультимножеств в состоянии алгоритма не превосходит $H$ (иначе мы за одну операцию ввода-вывода добавили в состояние больше $1$ мультимножества, что невозможно).

Шаг 5. Как может меняться состояние алгоритма в зависимости от операции?

• Read - мы вытаскиваем произвольный блок из состояния (не больше $H$ вариантов) и вставляем его в произвольное место внутренней памяти (в точности $C_{M}^B$ вариантов).
• Write - мы вытаскиваем произвольный блок из внутренней памяти (в точности $C_{M}^B$ вариантов) и вставляем его в произвольное место состояния между существующими блоками (не больше $H$ вариантов) или заменяем произвольный блок состояния (еще не больше $H$ вариантов).

Итого после одной произвольной операции состояние может стать одним из $3H C_M^B$ возможных. Соответственно после $H$ операций состояние может стать одним из $(3H C_M^B)^{H}$, а имея $H < n^2$ получаем верхнюю оценку в $(3n^2 C_M^B)^{H}$.

Шаг 6. Алгоритм обязан уметь генерировать каждую из возможных перестановок. Всего перестановок $n!$, но различаемых из них всего лишь $\frac{n!}{(B!)^{\frac{N}{B}}}$, поскольку блоки размера $B$ не различимы (с точки зрения того, что блоки размера $B$ могут быть переставлены за 1 операцию).

Шаг 7. Таким образом, мы получили неравенство: количество возможных состояний алгоритма (как его выход) должно быть больше количества различимых перестановок, то есть:

\[(3n^2 C_M^B)^{H} \geq \frac{n!}{(B!)^{\frac{N}{B}}}\]

Или, взяв логарифм:

\[H \ln \left((3n^2)C_M^B\right) \geq \ln n! - \frac{N}{B} \ln B!\]

Мы получим оценку на $H$ с помощью оценки факториала формулой Стирлинга снизу и $n^n$ сверху:

\[n \ln n - n < \ln n! < n \ln n\]

И, как следствие, опуская технические детали, $\ln C_n^k \geq k \ln \frac{n}{k} - n$.

Тогда левую часть без $H$ мы можем оценить снизу как:

\[\ln \left((3n^2)C_M^B\right) \geq \ln 3n^2 + B \ln \frac{M}{B}\]

А правую часть неравенства оценить сверху как:

\[\frac{n!}{(B!)^{\frac{N}{B}}} \leq N \ln \frac{N}{B} + N \leq 2 N \ln \frac{N}{B}\]

Таким образом мы получили неравенство:

\[H \left(\ln 3n^2 + B \ln \frac{M}{B} \right) \geq 2 N \ln \frac{N}{B}\]

Или

\[H \geq \frac{2N \ln \frac{N}{B}}{\ln 3n^2 + B \ln \frac{M}{B}}\]

Осталось рассмотреть два случая:

1. $\ln 3n^2 > B \ln \frac{M}{B}$ - тогда оцениваем знаменталь как $2 \ln 3n^2$, а вся дробь, опуская константы, $\frac{N \ln \frac{N}{B}}{\ln N} \leq N = \Omega(N)$ случай
2. $B \ln \frac{M}{B} > \ln 3n^2$ - тогда оцениваем знаменталь как $2B \ln \frac{M}{B}$, а вся дробь $\frac{N \ln \frac{N}{B}}{B \ln \frac{M}{B}} = \frac{N}{B} \log_{\frac{M}{B}} \frac{N}{B}$ по свойствам логарифмов, получили второй случай $\Omega(\frac{N}{B} \log_{\frac{M}{B}} \frac{N}{B})$.

Таким образом, мы получили два случая, которые в точности совпадают с нижней оценкой времени работы алгоритма, который мы получили примером в начале.

Ссылки

1. Конспекты профессора Yufei Tao из Chinese University of Hong Kong
2. Оригинальная работа A. Aggarwal and J. S. Vitter. The input/output complexity of sorting and related problems. CACM, 31(9):1116–1127, 1988.