Динамика по подмножествам и по изломанному профилю
Оглавление
Запись занятия
Задача коммивояжера
Во взвешенном графе необходимо проложить маршрут кратчайшей длины, посещающий все вершины, при том каждую только один раз.
Решение
Пусть dp[mask][v] - это кратчайший путь, посещающий все вершины из $mask$ и заканчивающийся в вершине $v$. Mask (маска) - это последовательность из $n$ нулей и единиц. Здесь и далее мы будем говорить, что вершина лежит в маске, если на её позиции стоит единица.
Переходы в динамике вполне очевидны: $dp[mask][v] \to dp[mask + u-тая вершина][u] + adj[v][u]$, где $adj[v][u]$ - вес ребра между вершинами $v$ и $y$. Или, на C++, так:
1
2
new_mask = mask | (1 << u);
dp[new_mask][u] = min(dp[new_mask][u], dp[mask][v] + adj[v][u])
Таким образом мы найдем ответ за время O(2^n \cdot n^2), так как в динамике $2^{n}\cdot n$ состояний и из каждого $n$ переходов.
Код
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <iostream>
#include <vector>
#include <algorithm>
#include <fstream>
#include <random>
#include <queue>
#include <cstring>
using namespace std;
const int N = 19;
int a[N][N];
int dp[(1 << N)][N];
const int INF = 2e9;
signed main() {
cin.tie(0);
ios_base::sync_with_stdio(0);
int n;
cin >> n;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
cin >> a[i][j];
}
}
int P = 1 << n;
for (int mask = 0; mask < P; ++mask) {
for (int i = 0; i < n; ++i) {
dp[mask][i] = INF;
}
}
for (int i = 0; i < n; ++i) {
dp[1 << i][i] = 0;
}
for (int mask = 0; mask < P; ++mask) {
for (int i = 0; i < n; ++i) { // последняя вершина в пути
for (int j = 0; j < n; ++j) {
if (((mask >> i) & 1) && ((mask >> j) & 1) == 0) {
dp[mask | (1 << j)][j] = min(dp[mask | (1 << j)][j], dp[mask][i] + a[i][j]);
}
}
}
}
int best_end = 0;
for (int i = 0; i < n; ++i) {
if (dp[P - 1][i] < dp[P - 1][best_end]) {
best_end = i;
}
}
cout << dp[P - 1][best_end] << '\n';
vector<int> ans;
int mask = P - 1;
for (int i = 0; i < n; ++i) {
ans.push_back(best_end);
int old_mask = mask ^ (1 << best_end);
for (int j = 0; j < n; ++j) {
if (dp[old_mask][j] + a[j][best_end] == dp[mask][best_end]) {
best_end = j;
break;
}
}
mask = old_mask;
}
for (int i = n - 1; i >= 0; --i) {
cout << ans[i] + 1 << ' ';
}
}
Симпатичные узоры-2
Нужно найти количество способов замостить поле $n \times m$ ($nm \leq 200$) чёрными или белыми клеточками $1 \times 1$ так, чтобы не было поля $2\times 2$ из одного цвета.
Решение
Из ограничений следует, что $\min(n, m) \leq 14$. Пусть без ограничения общности $n \leq 14$.
Мы будем считать количество способов замостить поле “по слоям” из $m$, или иначе говоря по “профилям”, то есть сначала для $m=1$, затем для $m=2$ и т.д. Конечно же, мы можем в лоб прикладывать один профиль к другому, проверяя нет ли в них одноцветного квадрата $2\times 2$, но это долго, ведь различных профилей $2^{14}$ (каждый цвет $0$ или $1$), а нам нужно квадрат количества профилей переходов, то есть $2^{28}$.
Чтобы эффективно считать такую ДП, внутри профиля мы будем поддерживать “излом” - это место, где профиль изгибается:
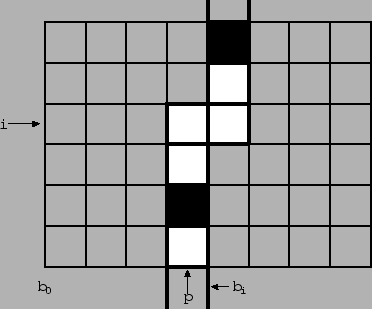
Такое состояние будет кодироваться парой $(mask, i)=(33, 2)$ где $i$ - место, где профиль изломался. Ну и, очевидно, что мы будем увеличивать $i$ внутри одного профиля так, чтобы к в конце у нас получился полноценный профиль без излома.
Вернёмся к задаче. Мы хотим уметь делать все переходы из состояния $(mask, i)$. Для этого нужно покрасить в какой-то цвет клетку,где ломается профиль. Но мы должны соблюсти условие, что не должно быть одноцветного квадрата $2 \times 2$. К сожалению, для этого придется ввести ещё одну размерность $c \in [0;1]$ - цвет клетки по диагонали от излома. Теперь информации достаточно, чтобы понимать, в какие цвета можно красить клетку на изломе профиля.
Например, мы можем покрасить клетку на изломе в цвет 0, если $c = 1$ или в $mask$ на позиции $i$ или $i-1$ стоит $1$. Аналогично с цветом $0$.
Так же при написании ДП по изломанному профилю стоит обратить внимание на переходы от одного профиля к другому, они становятся не такими тривиальными. Более подробно - см. реализацию.
Код
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include <iostream>
#include <vector>
#include <cassert>
#include <set>
#include <cstring>
using namespace std;
// dp[mask][c][i]
const int N = 14;
int dp[1 << N][2][N + 1], newdp[1 << N][2][N + 1];
const int MOD = (1 << 30) + 1;
int main() {
int n, m;
cin >> n >> m;
if (n > m) {
swap(n, m);
}
// n <= m
if (m == 1) { // n = m = 1
cout << 2;
return 0;
}
int p = 1 << n;
for (int mask = 0; mask < p; ++mask) {
for (int c = 0; c < 2; ++c) {
dp[mask][c][1] = 1;
}
}
for (int layer = 1; layer < m; ++layer) {
for (int i = 1; i < n; ++i) {
for (int mask = 0; mask < p; ++mask) {
for (int c = 0; c < 2; ++c) {
if (((mask >> i) & 1) || ((mask >> (i - 1)) & 1) || c) {
dp[mask & ~(1 << i)][(mask >> i) & 1][i + 1] = (dp[mask & ~(1 << i)][(mask >> i) & 1][i + 1] + dp[mask][c][i]) % MOD;
}
if (((mask >> i) & 1) == 0 || ((mask >> (i - 1)) & 1) == 0 || c == 0) {
dp[mask | (1 << i)][(mask >> i) & 1][i + 1] = (dp[mask | (1 << i)][(mask >> i) & 1][i + 1] + dp[mask][c][i]) % MOD;
}
}
}
}
if (layer == m - 1) {
int ans = 0;
for (int c = 0; c < 2; ++c) {
for (int mask = 0; mask < p; ++mask) {
ans = (ans + dp[mask][c][n]) % MOD;
}
}
cout << ans;
return 0;
}
memset(newdp, 0, sizeof newdp);
for (int c = 0; c < 2; ++c) {
for (int mask = 0; mask < p; ++mask) {
newdp[mask & ~(1)][mask & 1][1] = (newdp[mask & ~(1)][mask & 1][1] + dp[mask][c][n]) % MOD;
newdp[mask | 1][mask & 1][1] = (newdp[mask | 1][mask & 1][1] + dp[mask][c][n]) % MOD;
}
}
memcpy(dp, newdp, sizeof newdp);
}
}
