Динамика по подмножествам
Оглавление
Запись занятия
Немного о том, как хранятся целые числа в этих ваших копутерах
В двоичной системе счисления числа записываются с помощью двух символов (0 и 1). Чтобы не путать, в какой системе счисления записано число, его снабжают указателем справа внизу. Например, число в десятичной системе 510, в двоичной 1012. Иногда двоичное число обозначают префиксом 0b, например 0b101.
В двоичной системе счисления (как и в других системах счисления, кроме десятичной) знаки читаются по одному. Например, число 1012 произносится «один ноль один».
Натуральные числа
Натуральное число, записываемое в двоичной системе счисления как (an-1an-2… a1a0)2, имеет значение:
(an-1an-2... a1a0)2 = a0 + 2a1 + 22a2 + ... + 2n-1an-1
где:
n — количество цифр (знаков) в числе,
ak — значения цифр из множества {0,1},
k — порядковый номер цифры
А как их хранить?
В компьютерах числа хранятся в двоичной записи. Проще всего хранить натуральные числа: нужно лишь запомнить последовательность из нулей и единиц. К сожалению, мы не можем хранить неограниченно большое число, ниже вы увидите таблицу для ограничений типов в C++:
| Тип данных | Размер, бит | Ограничения в степенях двойки | Примерные ограничения |
|---|---|---|---|
| unsigned char | 8 | [0; 28 - 1] | [0; 255] |
| unsigned short | 16 | [0; 216 - 1] | [0; 65'535] |
| unsigned int | 32 | [0; 28 - 1] | [0; 4,2 * 109] |
| unsigned long long | 64 | [0; 264 - 1] | [0; 1,8 * 1019] |
Например, если вы напишете код
1
unsigned char x = 11;
То в памяти 11 будет храниться как 00001011.
Отрицательные целые числа
Первая идея, которая приходит в голову - это зарезервировать один бит под знак (например, старший). Такой подход называется “прямой код”, и при его использовании возникнет сразу две проблемы:
- Числа
00000000и10000000обозначают 0 и -0. То есть есть два обозначение одного и того же числа 0. - Другая проблема - это арифметические операции. Оказывается, их очень неудобно реализовывать, если старший бит будет отвечать за знак.
Но есть и несколько плюсов:
- Достоинства представления чисел с помощью кода с дополнением до единицы
- Простое получение кода отрицательных чисел.
- Из-за того, что 0 обозначает +, коды положительных чисел относительно беззнакового кодирования остаются неизменными. Количество положительных чисел равно количеству отрицательных.
Всё же оказывается, что данный подход не применим для архитектуры компьютера, поэтому люди придумали решение, именуемое “дополнительный код”:
Будем хранить “остатки” от деления на 28 (или нужную степень двойки). Таким образом, если мы хотим сохранить число x от 0 до 127, то мы будем хранить именно его. Для чисел x из интервала [-128; -1] будем хранить его остаток от деления на 256, что эквивалентно числу 256 + x. Таким образом мы решили сразу две проблемы (вторая проблема решена, автоматически, так как арифметика остатков очень простая).
Таким образом, если вы напишете
1
char x = -2;
То в x будет записан в памяти как 256 - 2 = 254: 11111110
Преимущества данного подхода:
- Возможность заменить арифметическую операцию вычитания операцией сложения и сделать операции сложения одинаковыми для знаковых и беззнаковых типов данных, что существенно упрощает архитектуру процессора и увеличивает его быстродействие.
- Нет проблемы двух нулей.
Недостатки:
- Ряд положительных и отрицательных чисел несимметричен, но это не так важно: с помощью дополнительного кода выполнены гораздо более важные вещи, желаемые от способа представления целых чисел.
- В отличие от сложения, числа в дополнительном коде нельзя сравнивать как беззнаковые, или вычитать без расширения разрядности.
| Тип данных | Размер, бит | Ограничения в степенях двойки | Примерные ограничения |
|---|---|---|---|
| char | 8 | [-27; 27 - 1] | [-128; 127] |
| short | 16 | [-215; 215 - 1] | [-32768; 32767] |
| int | 32 | [-231; 231 - 1] | [-2,1 * 109; 2,1 * 109] |
| long long | 64 | [-263; 263 - 1] | [-9 * 1018; 9 * 1018] |
Обратите внимаение, здесь в таблице нет типа long. Он равен обычному int и его никогда не стоит использовать!
Упражнения на битовые операции
Теперь вы формально знаете, как хранятся числа в двоичной записи. Настало время этим воспользоваться.
Битовые операции в C++
Есть несколько видов битовых операций: логические или, и, ксор и отрицание. Они выполняют логические операции над каждым битом независимо. На C++ это будет соответственно так:
1
2
3
4
5
6
char a = 0b0011; // 3
char b = 0b0101; // 5
char c = a | b; // 0011 | 0101 = 0111 = 7
char d = a & b; // 0011 & 0101 = 0001 = 1
char e = a ^ b; // 0011 ^ 0101 = 0110 = 6
char g = ~a; // ~00000011 = 11111100 = -4
Кроме того, часто пригождается еще и операции битового сдвига влево и вправо соответственно:
1
2
char h = a << 2; // 11 << 2 = 1100 = 12
char i = b >> 2; // 101 >> 2 = 1
С помощью таких примитивов предлагается решить несколько упражнений:
Как получить 2n?
Решение
1
2
int x = 1 << n;
long long y = 1LL << n;
Как убрать последнюю единицу в битовой записи?
Решение
1
2
int x = 228;
int y = x & (x - 1); // x без последней единицы в битовой записи
Как убрать группу из единиц на конце числа?
1
2
int x = 7 + 32;
int y = x & (x + 1); // x без группы из единиц на конце числа, т.е. 32
ДП по подмножествам
Задача коммивояжера. Во взвешенном графе необходимо проложить маршрут кратчайшей длины, посещающий все вершины, при том каждую только один раз.
Решение
Пусть dp[mask][v] - это кратчайший путь, посещающий все вершины из mask и заканчивающийся в вершине v. Mask (маска) - это последовательность из n нулей и единиц. Здесь и далее мы будем говорить, что вершина лежит в маске, если на её позиции стоит единица.
Переходы в динамике вполне очевидны: dp[mask][v] -> dp[mask + u-тая вершина][u] + adj[v][u], где adj[v][u] - вес ребра между вершинами v и y. Или, на C++, так:
1
2
new_mask = mask | (1 << u);
dp[new_mask][u] = min(dp[new_mask][u], dp[mask][v] + adj[v][u])
Таким образом мы найдем ответ за время O(2n n 2), так как в динамике 2n n состояний и из каждой n переходов.
Код
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <iostream>
#include <vector>
#include <algorithm>
#include <fstream>
#include <random>
#include <queue>
#include <cstring>
using namespace std;
const int N = 19;
int a[N][N];
int dp[(1 << N)][N];
const int INF = 2e9;
signed main() {
cin.tie(0);
ios_base::sync_with_stdio(0);
int n;
cin >> n;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
cin >> a[i][j];
}
}
int P = 1 << n;
for (int mask = 0; mask < P; ++mask) {
for (int i = 0; i < n; ++i) {
dp[mask][i] = INF;
}
}
for (int i = 0; i < n; ++i) {
dp[1 << i][i] = 0;
}
for (int mask = 0; mask < P; ++mask) {
for (int i = 0; i < n; ++i) { // последняя вершина в пути
for (int j = 0; j < n; ++j) {
if (((mask >> i) & 1) && ((mask >> j) & 1) == 0) {
dp[mask | (1 << j)][j] = min(dp[mask | (1 << j)][j], dp[mask][i] + a[i][j]);
}
}
}
}
int best_end = 0;
for (int i = 0; i < n; ++i) {
if (dp[P - 1][i] < dp[P - 1][best_end]) {
best_end = i;
}
}
cout << dp[P - 1][best_end] << '\n';
vector<int> ans;
int mask = P - 1;
for (int i = 0; i < n; ++i) {
ans.push_back(best_end);
int old_mask = mask ^ (1 << best_end);
for (int j = 0; j < n; ++j) {
if (dp[old_mask][j] + a[j][best_end] == dp[mask][best_end]) {
best_end = j;
break;
}
}
mask = old_mask;
}
for (int i = n - 1; i >= 0; --i) {
cout << ans[i] + 1 << ' ';
}
}
SOS dp
Sum over Subsets (SOS) dp - это техника, позволяющая найти сумму следующего вида:
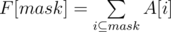
То есть для каждой маски найти сумму элементов на всех её подмасках.
Перебор всех подмасок данной маски
Сразу продемонстрируем способ:
1
2
for (int submask = mask; s; submask = (submask - 1) & mask)
F[mask] += A[submask]
Ок, почему это работает?
Пусть у нас есть текущая подмаска submask, и мы хотим перейти к следующей подмаске. Отнимем от маски submask единицу, тем самым мы снимем самый правый единичный бит, а все биты правее него поставятся в 1. Затем удалим все “лишние” единичные биты, которые не входят в маску mask и потому не могут входить в подмаску. Удаление осуществляется битовой операцией & mask. В результате мы “обрежем” маску submask-1 до того наибольшего значения, которое она может принять, т.е. до следующей подмаски после submask в порядке убывания.
Таким образом, этот алгоритм генерирует все подмаски данной маски в порядке строгого убывания, затрачивая на каждый переход по две элементарные операции.
При этом для каждой маски перебрать все её подмаски займет по времени O(3n). Почему? Приведем комбинаторное доказательство:
Каждый бит независимо может быть в одном из трех состояний: не в маске, в маске И подмаске одновременно или в маске, но не в подмаске, значит всего таких состояний 3n (потому что биты независимы), что и т.д.
SOS DP
Введём вспомогательное состояние, которое позволит считать сумму более эффективно. Пусть dp[mask][k] - это сумма на всех подмасках, которые отличаются от mask только в последних k битах (в 0-индексации). Например, если mask=101012, то dp[mask][3] будет отвечать за 4 подмаски: 100002, 100012, 101002 и 101012.
После того, как мы придумали состояние, придумать переходы не составляет труда: если на позиции k стоит 0, то и в подмасках на этой позиции должен стоять 0, т.е. переход в dp[mask][k-1], если же на позиции k стоит 1, то в подмасках может стоять как 0, так и 1. Т.е. мы можем либо занулить этот бит, либо оставить единичным: dp[mask ^ (1 « k)][k-1] + dp[mask][k-1].
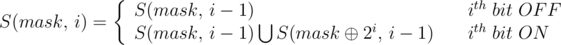
1
2
3
4
5
6
7
8
9
10
for (int mask = 0; mask < (1 << N); ++mask) {
dp[mask][-1] = A[mask];
for (int i = 0; i < N; ++i) {
if (mask & (1 << i))
dp[mask][i] = dp[mask][i - 1] + dp[mask ^ (1 << i)][i - 1];
else
dp[mask][i] = dp[mask][i - 1];
}
F[mask] = dp[mask][N - 1];
}
Можно заметить, что переходы по второй размерности ведут только в прошлый слой, а потому можно отказаться от неё:
1
2
3
4
5
6
7
for (int i = 0; i < (1 << N); ++i)
F[i] = A[i];
for (int i = 0; i < N; ++i)
for (int mask = 0; mask < (1 << N); ++mask) {
if (mask & (1 << i))
F[mask] += F[mask ^ (1 << i)];
}
